数据结构
- 线性结构 : 数组, 栈, 队列, 链表, 哈希表
- 树结构 : 二叉树, 二分搜索树, AVL, 红黑树, Treap, Splay, 堆, Trie, 线段树; K-D树, 并查集, 哈夫曼树
- 图结构 : 邻接矩阵, 邻接表
根据不同的场景, 灵活选择最适合的数据结构.
数据结构 + 算法 = 程序
数组 Array
Java的泛型, 不可以是基本数据类型, 只能是类对象.
简单的时间复杂度分析
- O(1), O(n), O(lgn), O(nlogn), O(n^2)
- O描述的是算法的运行时间和输入数据直接的关系.
public static int sum(int[] nums){
int sum = 0;
// 算法复杂度是 O(n) 的
// n 是 nums 中的元素个数
// 这个算法的运算和 n 是呈线性关系的
for(int num : nums) sum+=sum;
return sum;
}
是一个 渐进时间复杂度, 描述n趋近于无穷的情况.
算法的分析, 一般关注的是最坏的情况.
均摊复杂度(Amortized Time Complexity).
复杂度震荡
addLast 和 removeLast 切换进行, 每次都会是 O(n) 复杂度.
出现问题的原因: removeLast 时 resize 过于着急(Eager).
解决方案: Lazy. 1/4 的时候在缩容.
栈和队列
栈 Stack
也是一种线性结构, 相比数组, 栈对应的操作是数组的子集.
只能从一端添加元素, 也只能从一端取出元素. 入栈, 出栈.
这一端称为栈顶.
是一种后进先出的数据结构. Last In First Out(LIFO)
栈的应用
- Undo操作(撤销)
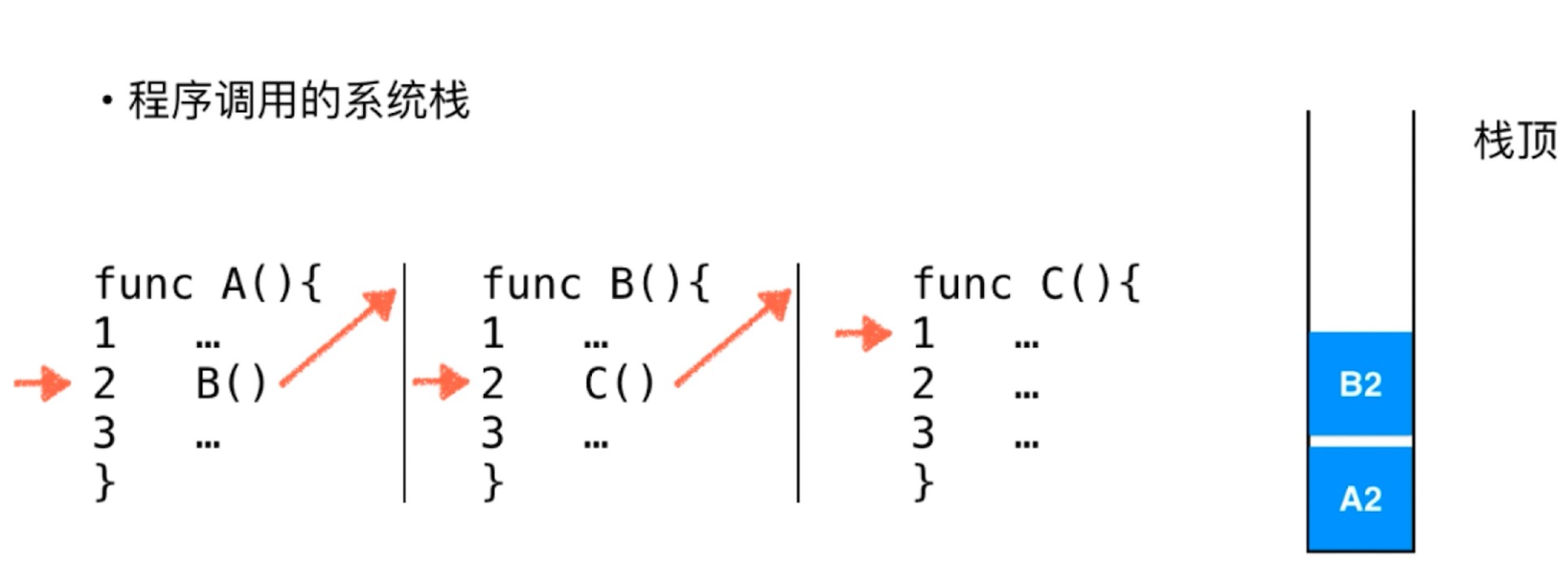
- 程序调用的系统栈
- 函数子过程调用, 可以把原来过程执行到哪里, 就压入系统栈, 方便在子过程调用结束之后找回原来的位置.
- 括号匹配 - 编译器
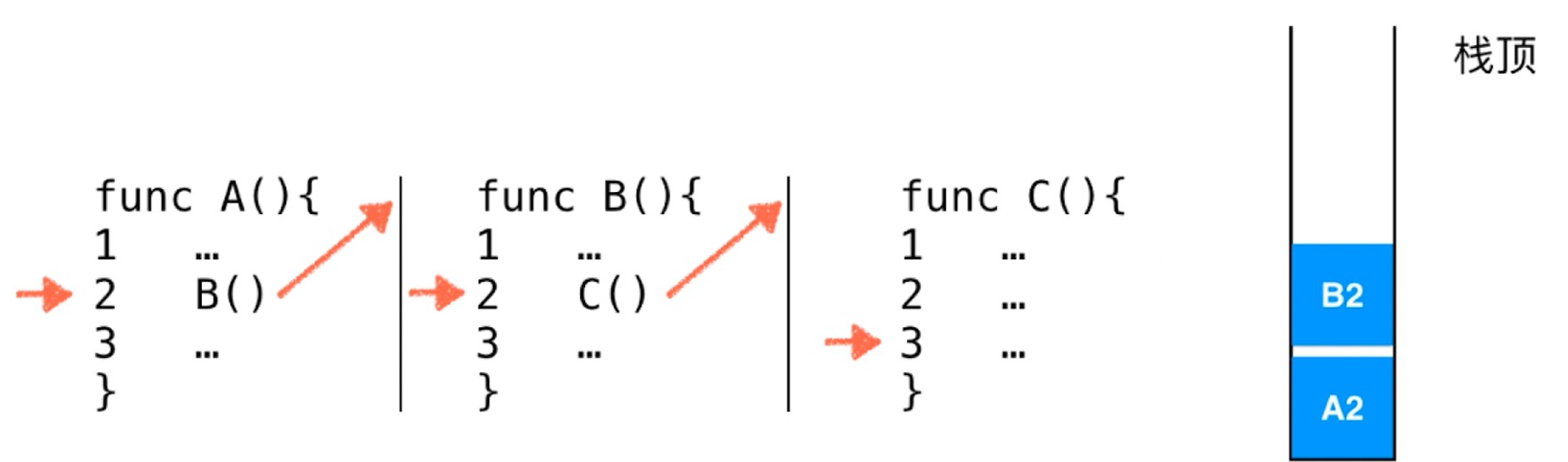
执行完C就可以继续执行B2了, 依次类推.
解决了子过程, 子逻辑的调用问题.
括号匹配
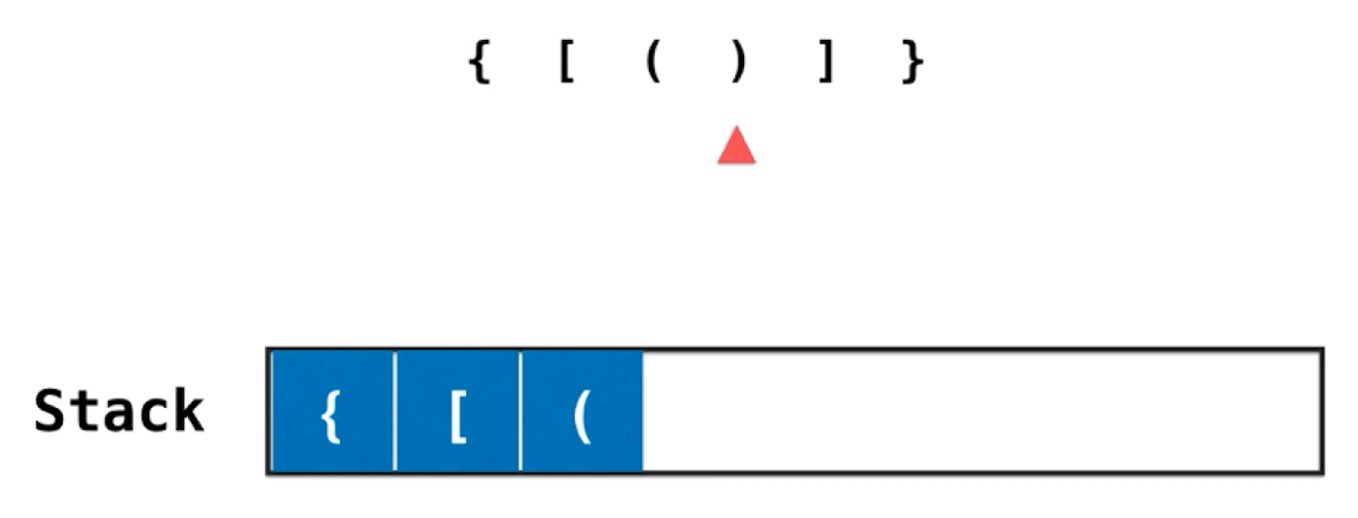
栈顶元素反映了在嵌套的层次关系中, 最近的需要的匹配的元素.
基于栈实现队列.
队列 Queue
也是一种线性结构.
相比数组, 队列对应的操作是数组的子集.
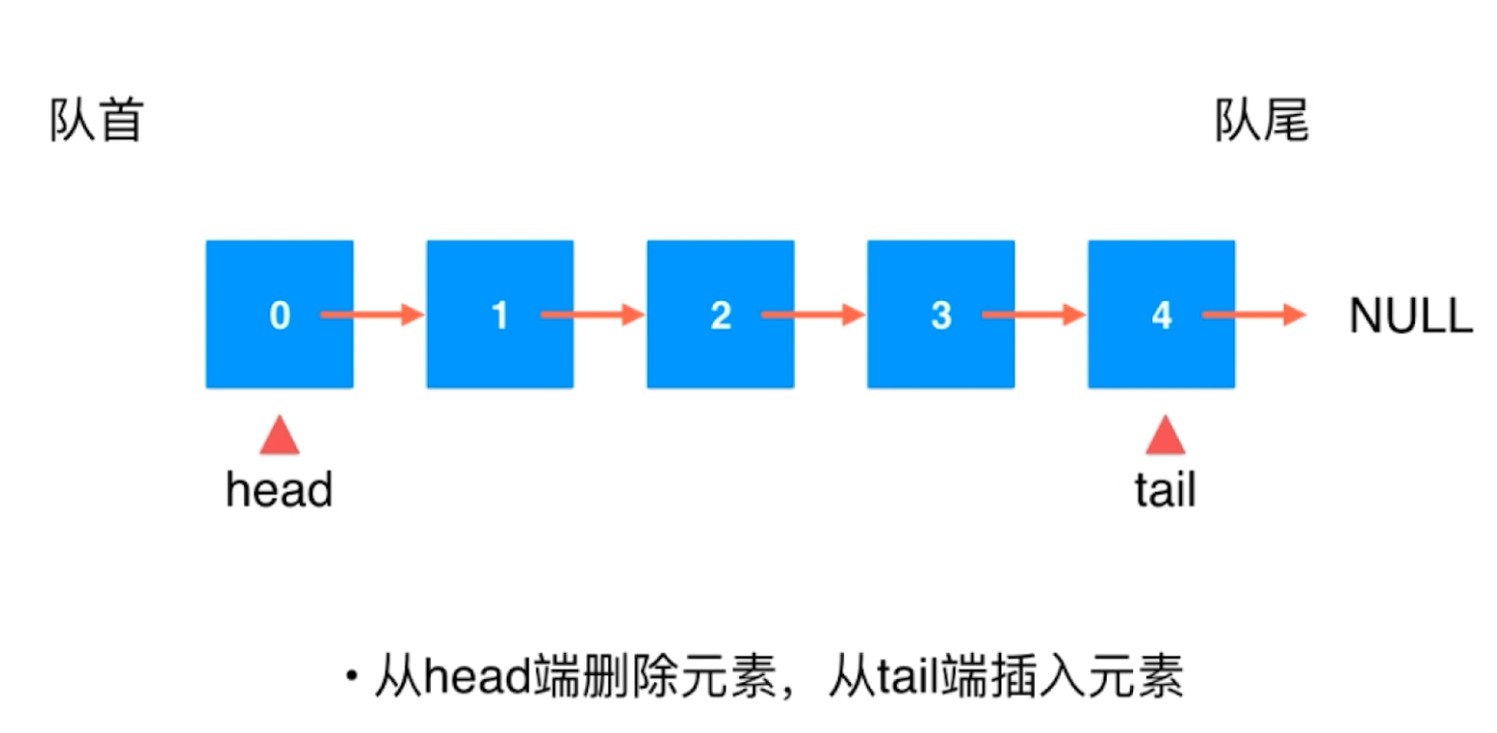
只能从一端(队尾)添加元素, 只能从另一端(队首)取出元素.
是一种先进先出的数据结构. First In First Out(FIFO).
数组队列的问题
删除队首元素, 时间复杂度变成 O(n) 级别. 循环队列可以解决该问题.
front == tail 队列为空. 入队就维护 tail . 出队就维护 front, 指向改变.
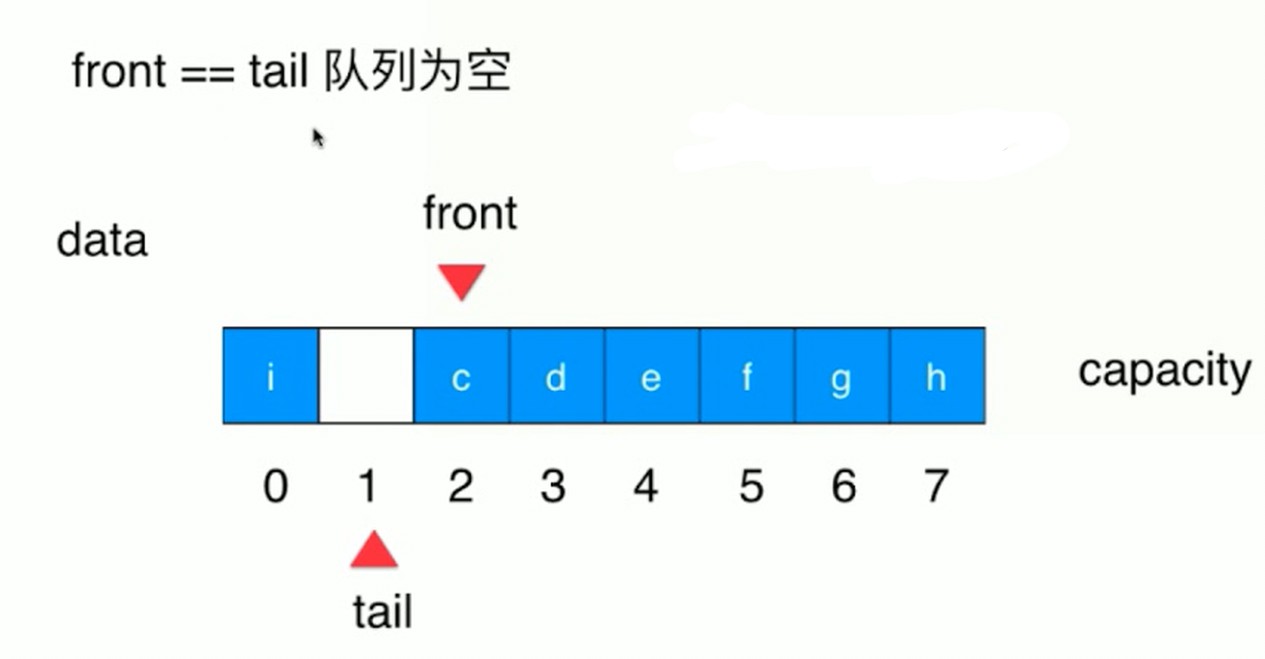
(tail + 1) % c == front 队列满. 也就是说 capacity 会浪费一个.
链表 Linked List
动态数组, 栈, 队列, 底层依托的都是静态数组, 靠 resize 解决固定容量问题.
链表是真正动态的数据结构. 最简单的动态数据结构.
更深入理解引用(或者指针)
更深入理解递归.
数据存储在”节点”(Node)中.
优点: 真正的动态, 不需要处理固定容量的问题.
缺点: 丧失了随机访问的能力.
数组和链表对比
- 数组最好用于索引有语意的情况.
- 最大优点: 支持快速查询.
- 链表不适合用于索引有语意的情况.
- 最大的优点: 动态.
链表的实现
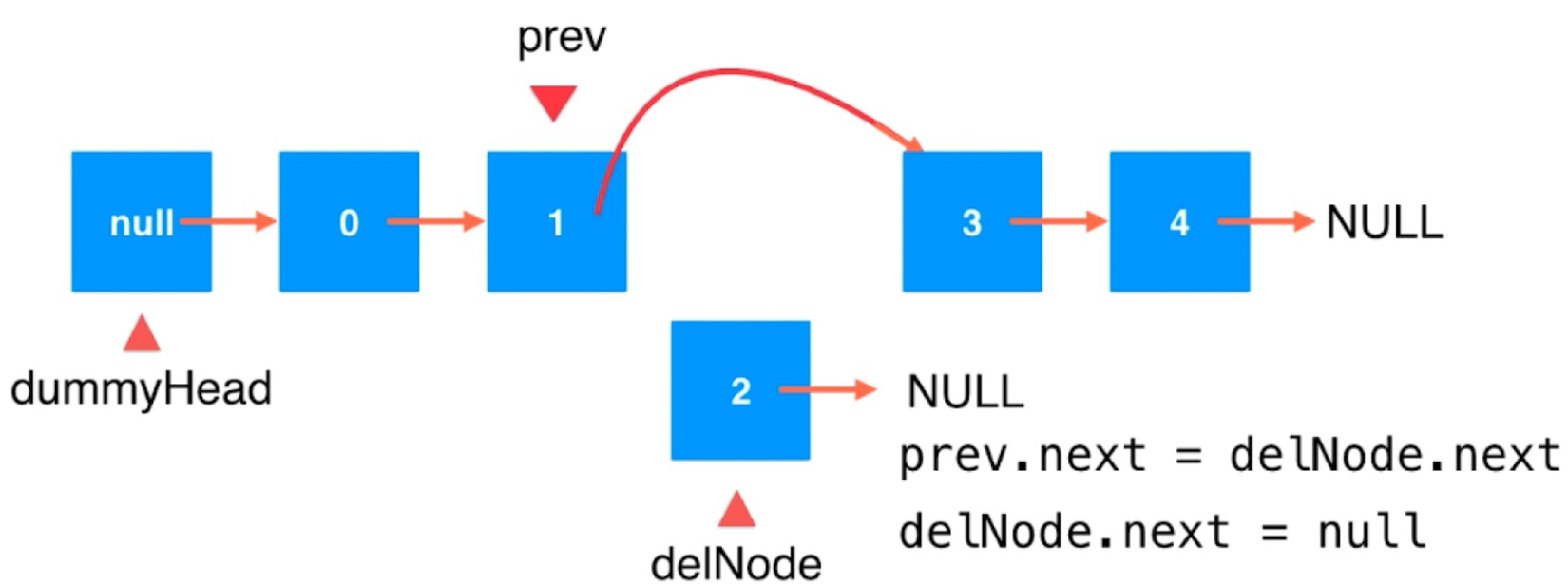
在指定位置插入元素是基于前一个节点位置的, 所以在链表头插入会有问题. 引入虚拟头节点解决.

基于链表实现栈
基于链表实现队列
双链表, 循环链表, 数组链表
递归 Recursion
递归很容易和树联系在一起. 在树中使用递归是很自然方便的.
本质上, 将原来的问题, 转换为更小的同一问题, 以此类推, 最后变成基本问题.
举例: 数组求和.

递归的基本原则
- 求解最基本问题.
- 把原问题转化成更小的问题.
注意递归函数的”宏观”语意.
递归函数就是一个函数, 完成一个功能.
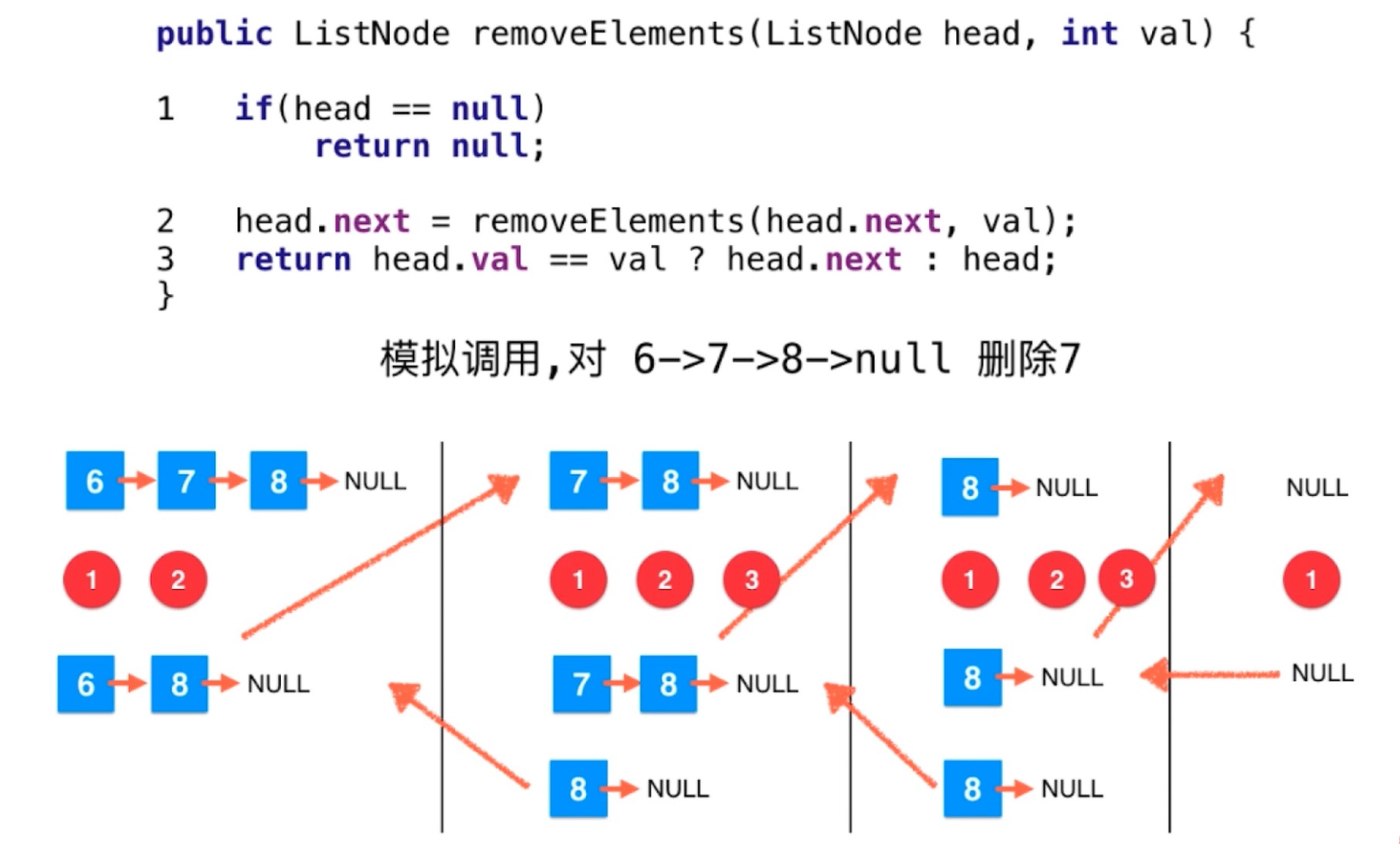
链表天然的递归性
e -> 一个更短的链表(少了一个节点) -> NULL
递归解决删除这个更小的链表中相应的元素.
递归的运行机制
递归的微观解读
- 递归函数的调用, 本质就是函数调用
- 只不过调用的函数是自己
数组求和

链表递归删除
递归调用是有代价的
函数调用 + 系统栈空间
二分搜索树 Binary Search Tree
应用场景: 目录
- 树结构本身就是一个天然的组织结构
- 将数据使用树结构存储后, 出奇的高效
二叉树
每个节点最多2个叉

- 和链表一样, 动态数据结构
- 二叉树具有唯一根节点
- 二叉树每个节点最多有两个子节点
- 二叉树每个节点最多一个父节点
- 二叉树具有天然递归结构
- 每个节点的左子树也是二叉树
- 每个节点的右子树也是二叉树
- 二叉树不一定是”满”的
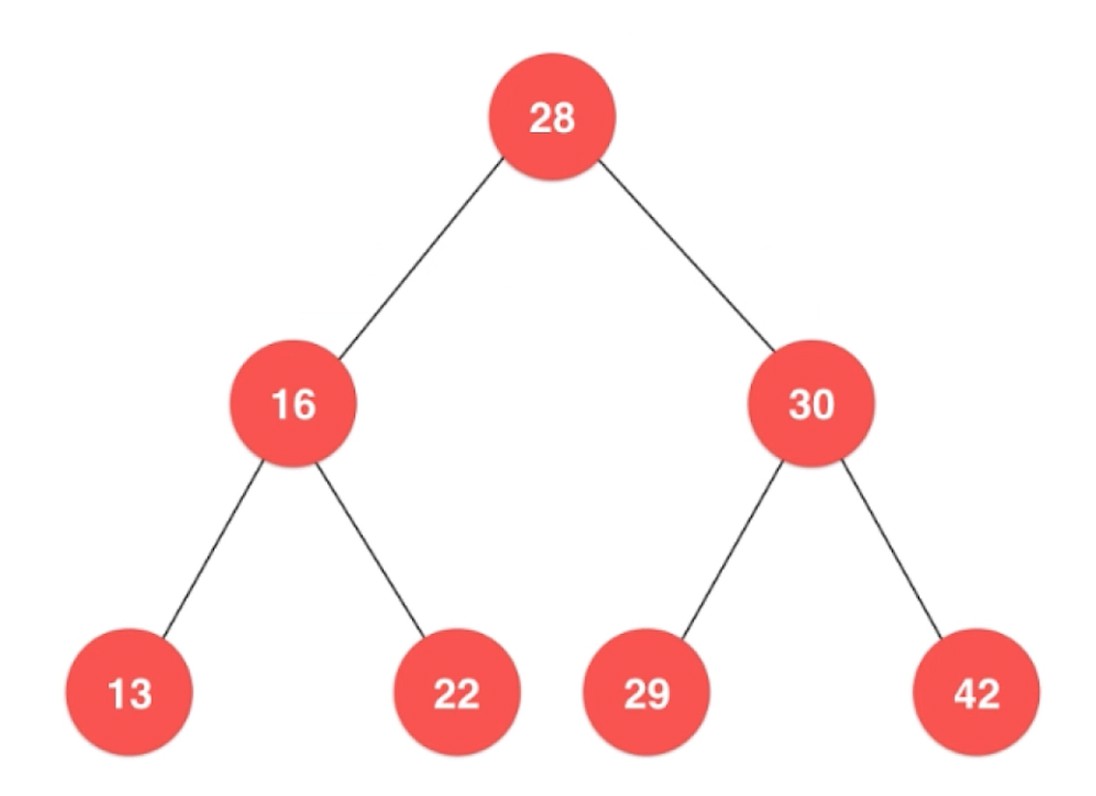
二分搜索树
- 二分搜索树是二叉树
- 二分搜索树的每个节点的值
- 大于其左子树的所有节点的值
- 小于其右子树的所有节点的值
- 每一棵子树也是二分搜索树
要有上述性质, 存储的元素必须有可比较性
- 例子中二分搜索树不包含重复元素
- 如果想实现, 改变定义即可
- 左子树小于等于节点; 右子树大于等于节点
二分搜索树的遍历
- 遍历操作就是把所有节点都访问一遍
- 对于遍历操作, 两棵子树都要顾及
- 本质是遍历到那个节点再进行操作
前序遍历: 先访问节点, 再访问左右节点
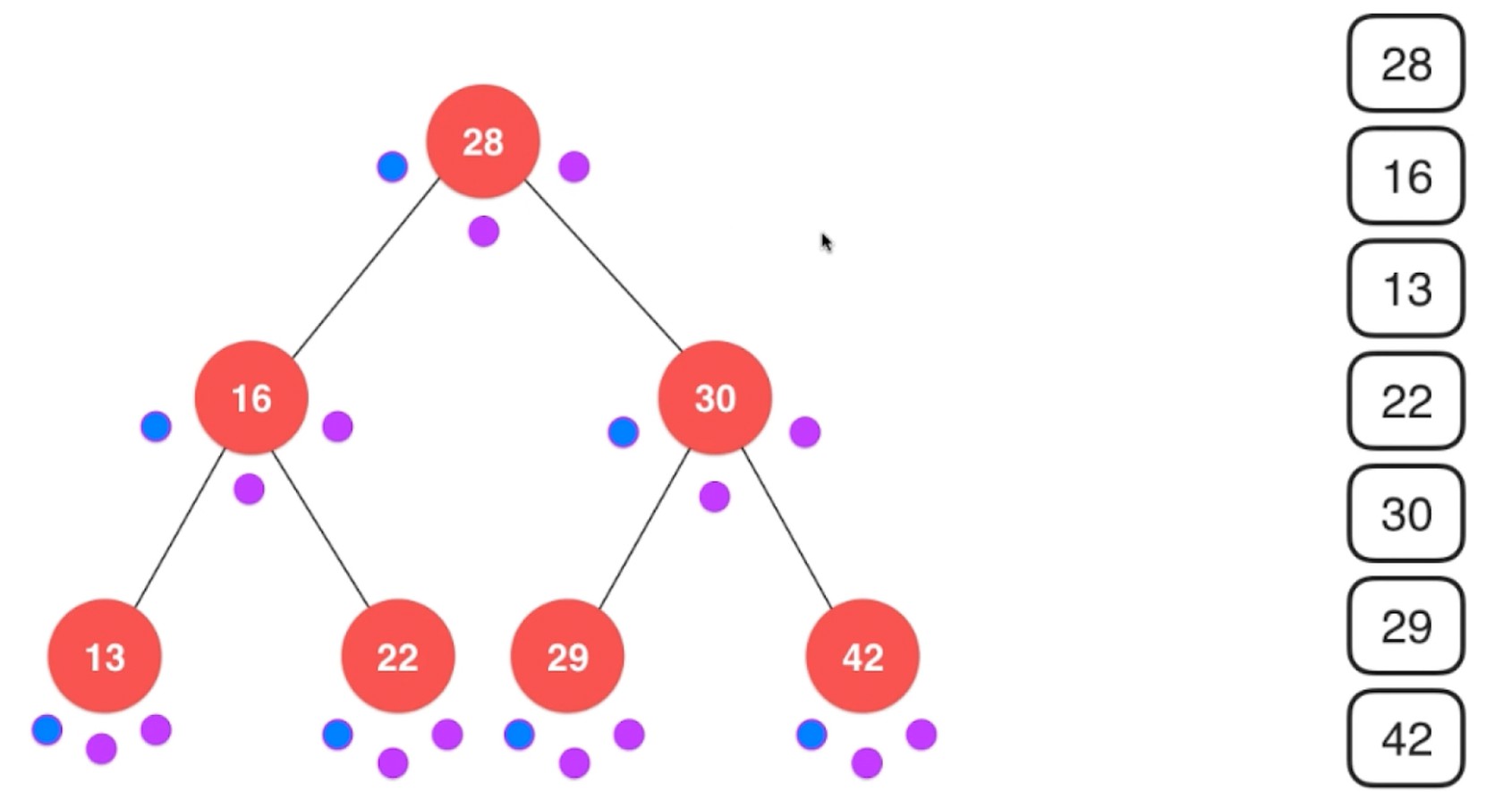
中序遍历
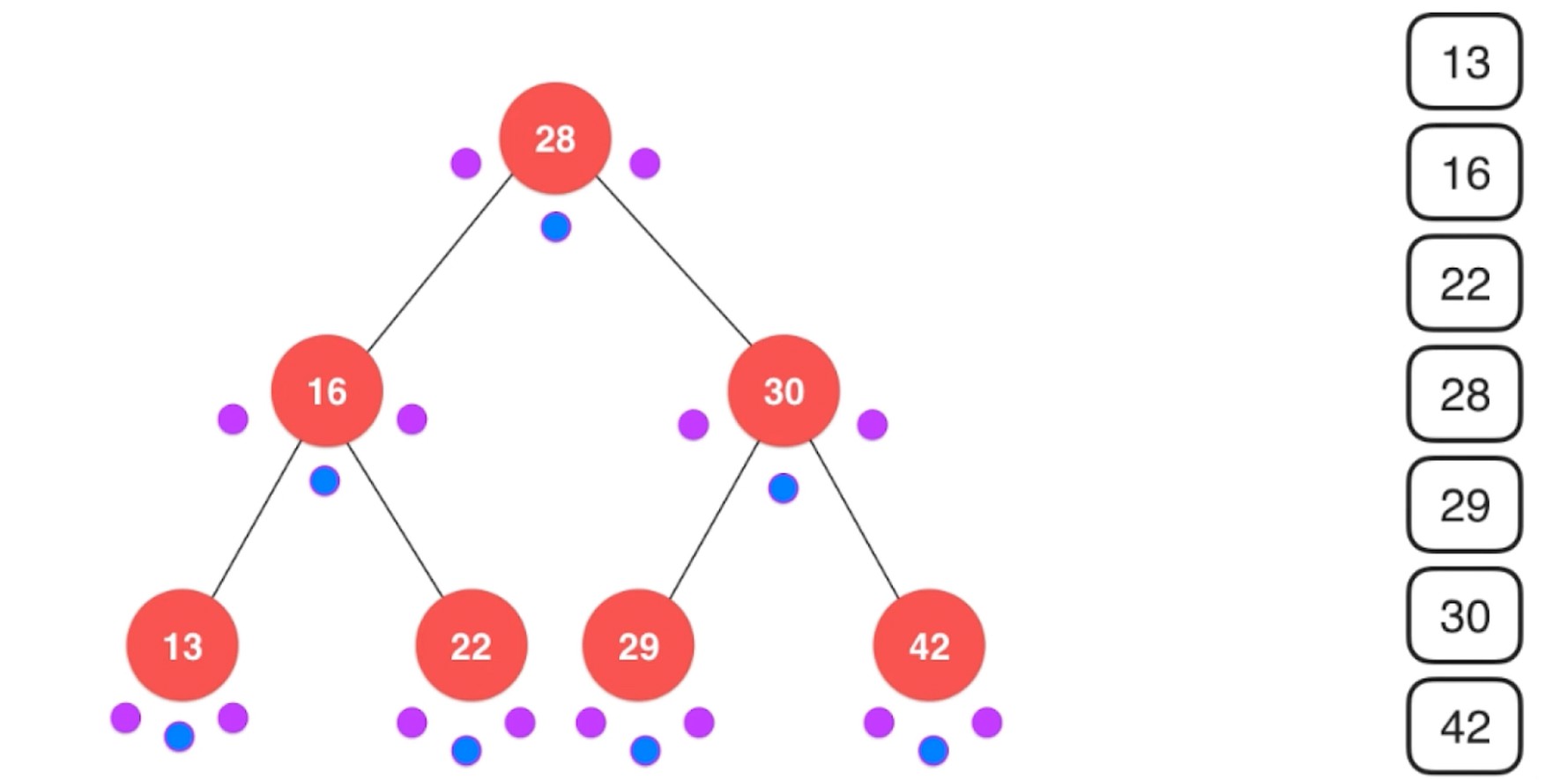
后序遍历. 可以为二分搜索树释放内存.
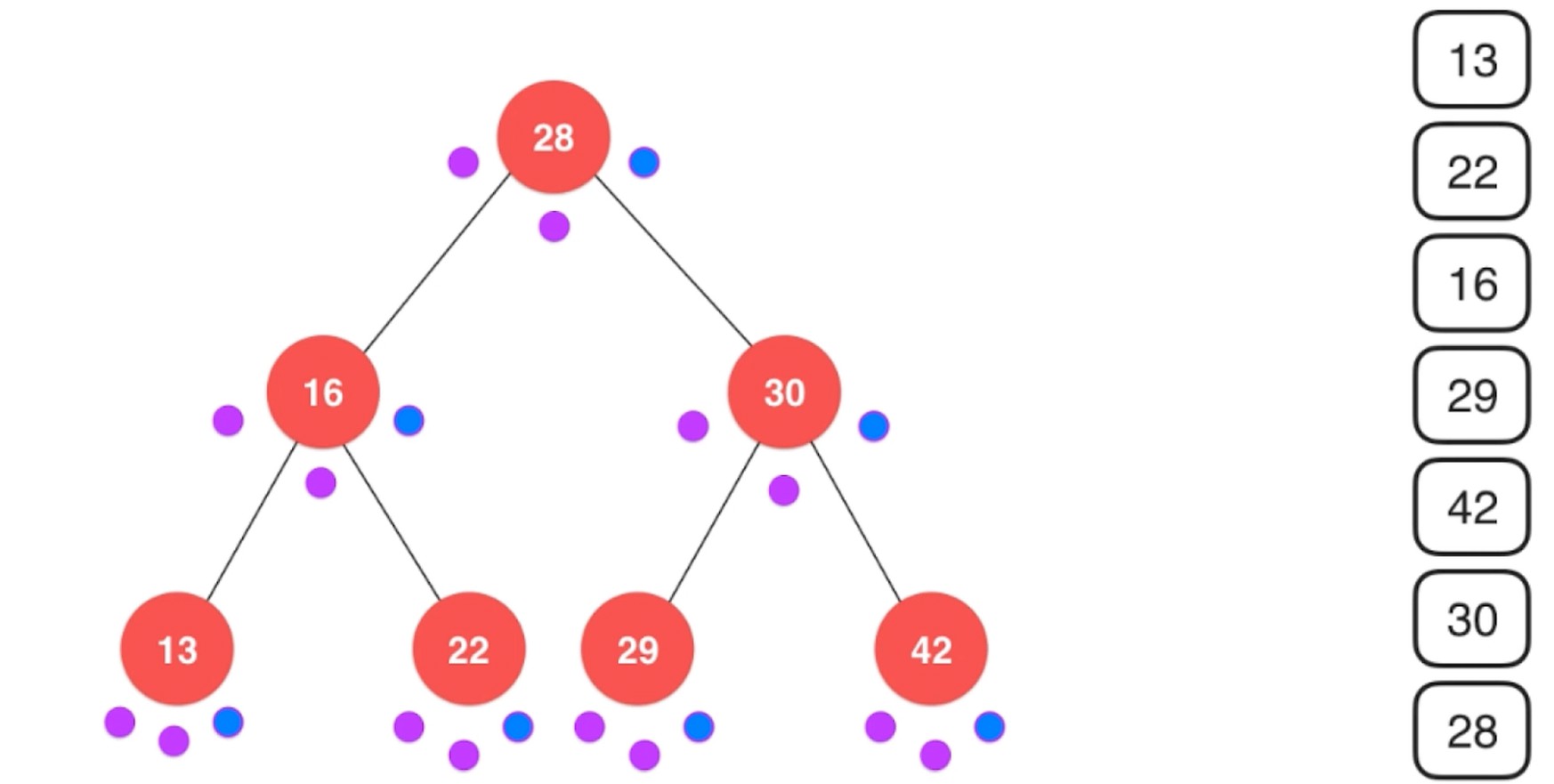
层序遍历
层序遍历, 又称为广度优先遍历.
使用队列实现.
常用于算法设计中 – 最短路径
删除元素
删除二分搜索树的最小值和最大值
最小值: 最左边的值
最大值: 最右边的值
删除任意节点
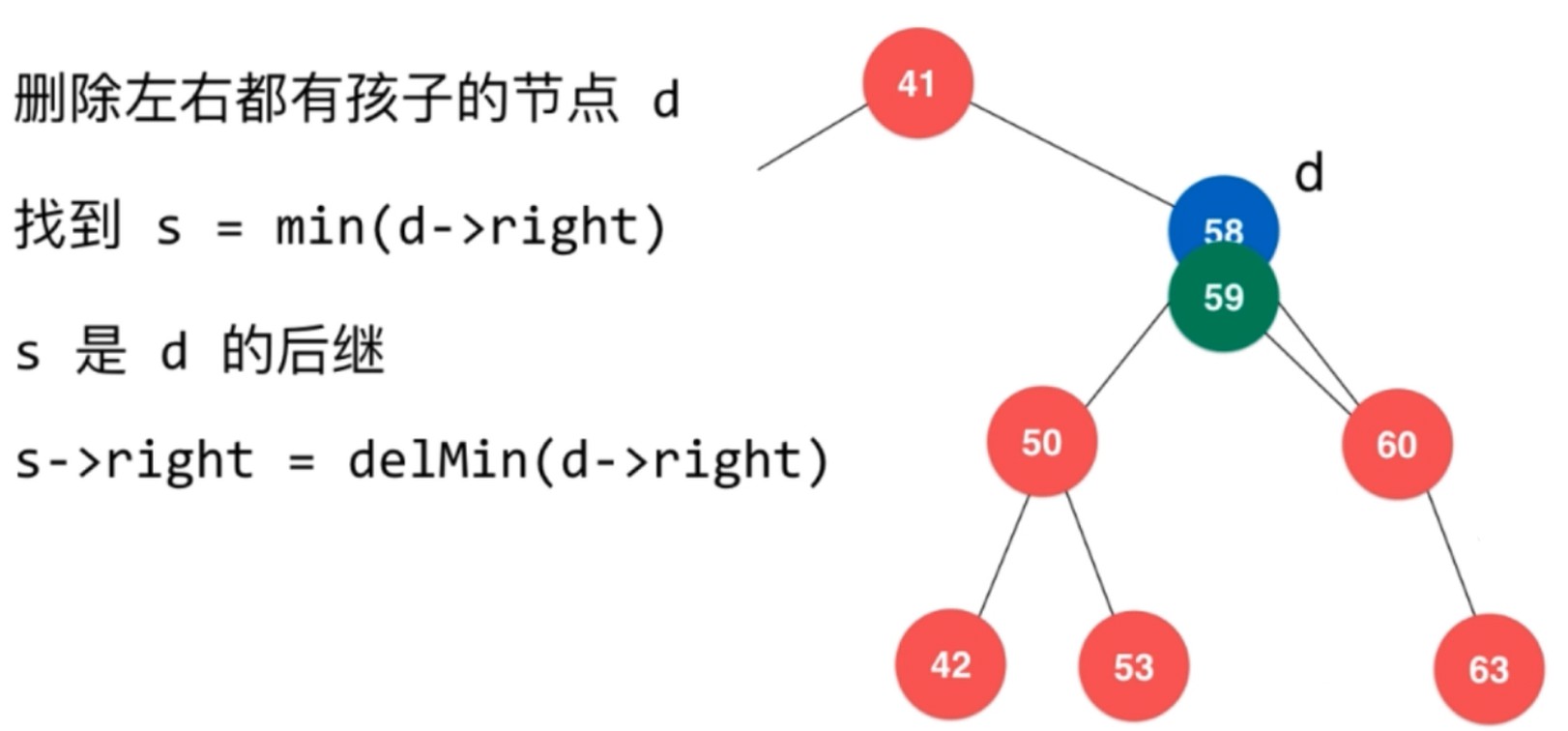
对于右边, 离删除节点最近的节点是 删除节点右节点树最左边的节点, 也就是它的后继.
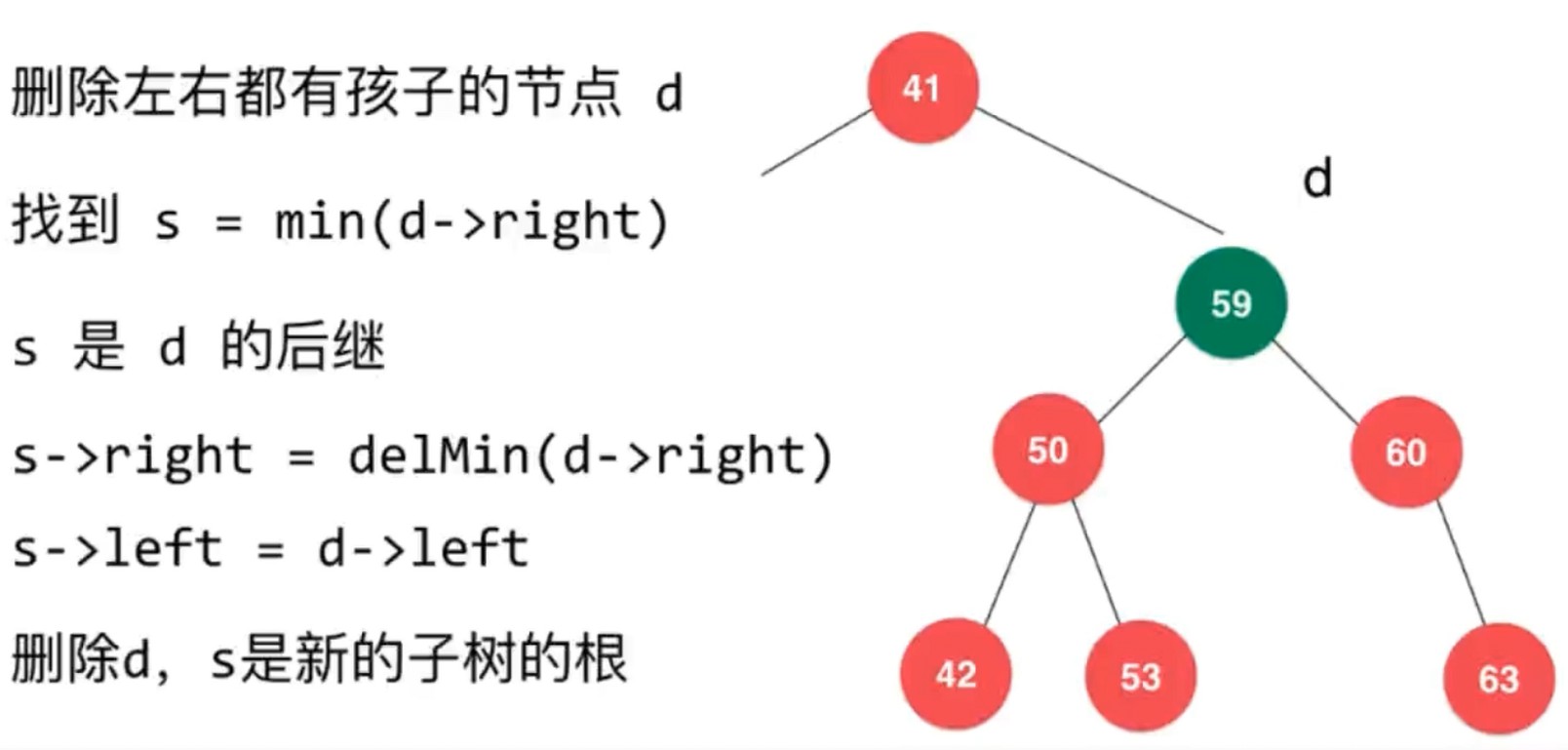
使用 前驱 也一样
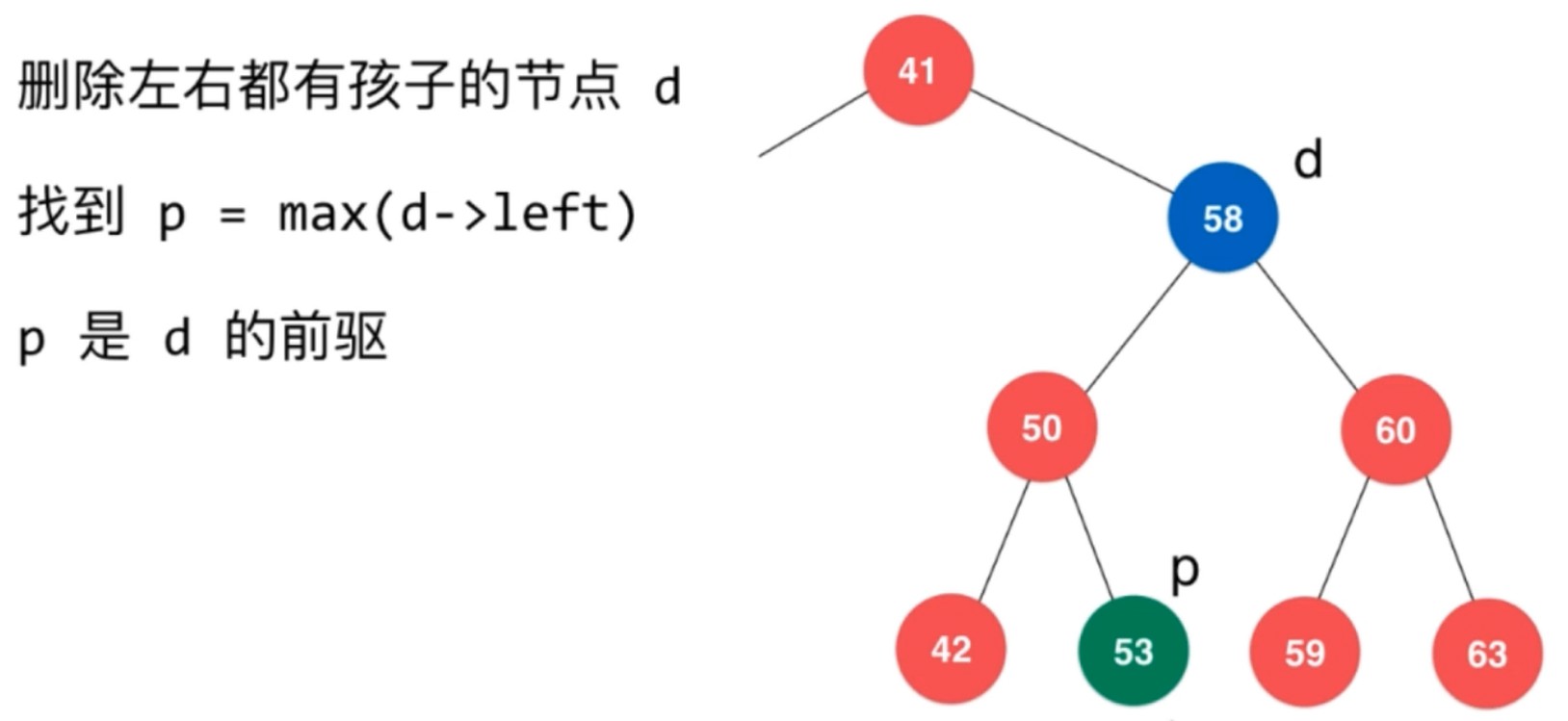
集合和映射 Set And Map
集合
高层数据结构. 不能放重复元素
Set<E>
- void add(E)
- void romove(E)
- boolean contains(E)
- int getSize()
- boolean isEmpty()
- 基于二分搜索树实现集合
- 基于链表实现集合
集合时间复杂度分析

二叉树节点数(满树)

n是节点数

logn和n的差距. 常数n一般不算.
二分搜索树最坏的情况: 所有节点在一个方向, 形成一个链表. 如果按顺序来创建的话, 二分搜索树就会退化成链表, 这样时间复杂度就是O(n)了.
解决方案: 平衡二叉树.
有序集合: 基于搜索树的实现
无序集合: 基于哈希表或链表的实现
多重集合: 集合中的元素可以重复
映射
在一些语言中叫做字典.
Key-Value
- 存储(键, 值)数据对的数据结构
- 根据键(Key), 寻找值(Value)
Map<K, V>
- void add(K, V)
- V remove(K)
- boolean contains(K)
- V get(K)
- void set(K, V)
- int getSize()
- boolean isEmpty()
基于链表和基于二分搜索树的映射时间复杂度

多重映射: 键可以重复.
优先队列和堆 PriorityQueue And Heap
堆
堆本身也是一棵树.
二叉堆 Binary Heap – 堆的一种实现方式
- 是一棵完全二叉树
- 完全二叉树: 把元素顺序排列成树的形状
- 堆中某个节点的值总是不大于父节点的值
- 最大堆(相应的也有最小堆)
- 低层的值不一定比高层的值大(节点的大小和层数没有必要的联系)
- 因为完全二叉树是按顺序来排的, 所以可以用数组来表示出来
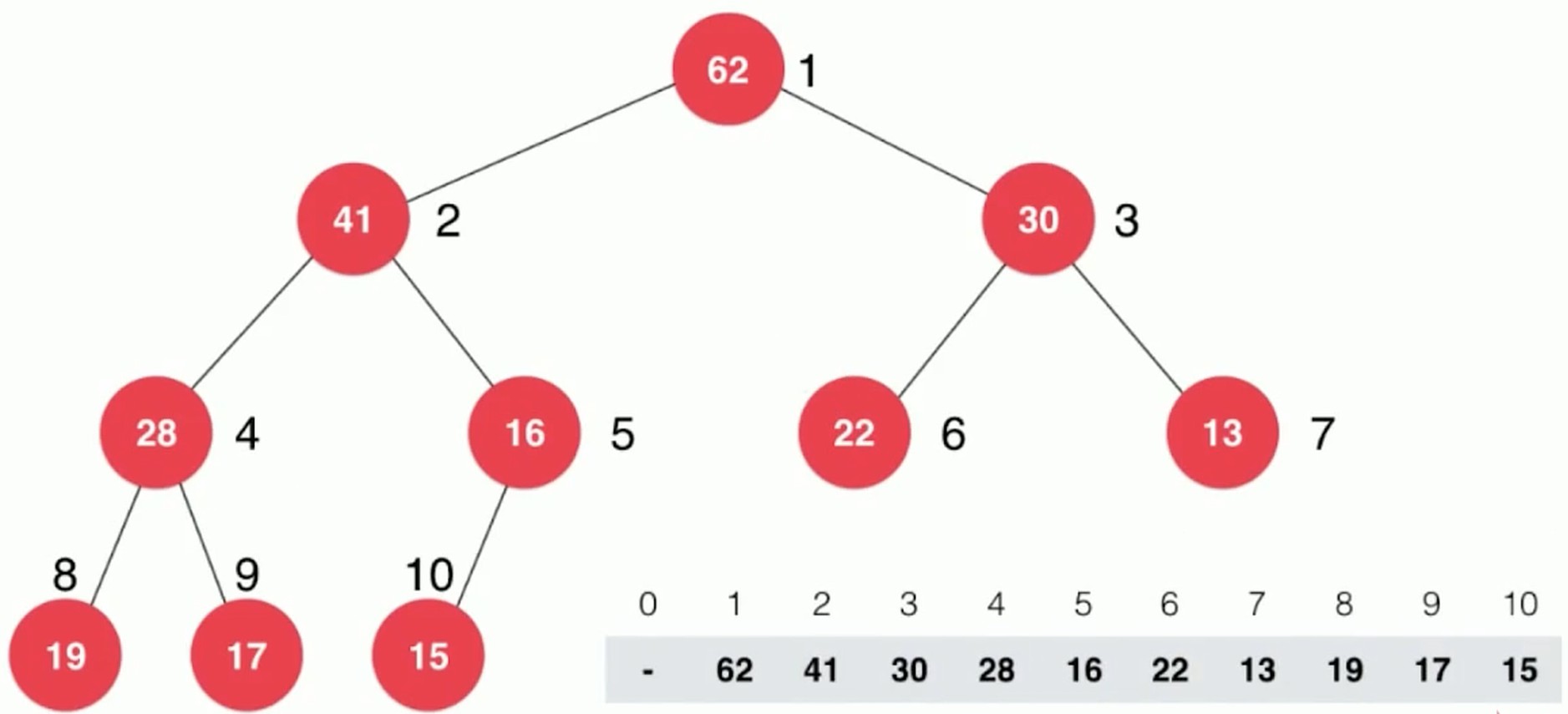
用数组存储二叉堆, 存在以下的关系, i是当前节点的下标.
- parent(i) = i / 2(注意向下取整)
- left child(i) = 2 * i
- right child(i) = 2 * i + 1
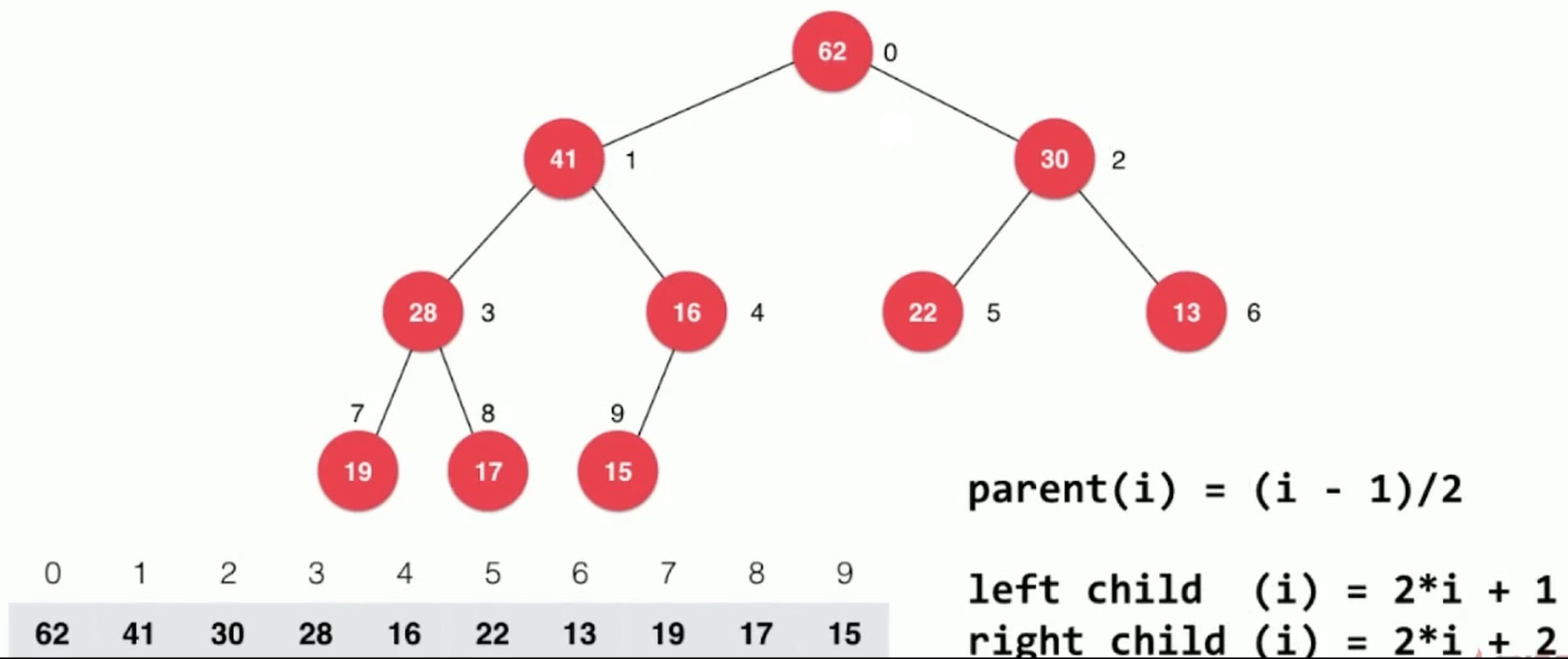
向堆中添加元素–Sift Up, 上浮
添加一个元素, 先在下一层添加新的元素, 然后与父节点进行比较, 如果大于, 向上移动(实际就是交换), 继续与父节点比较, 如果还是大于继续向上, 以此类推.
从堆中取出元素–Sift Down, 下沉
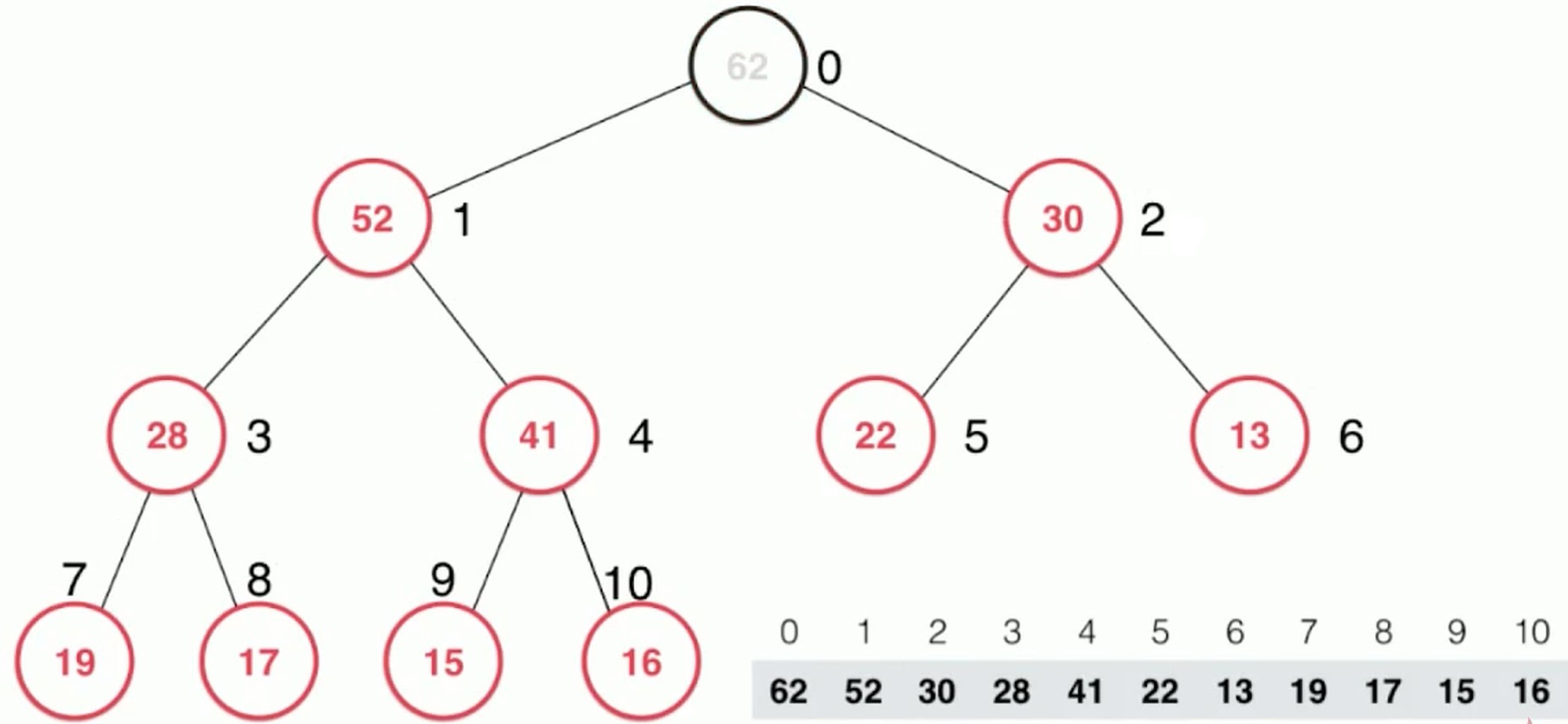
把最后一个元素放在堆顶, 然后向下比较, 与两个节点中较大的进行交换位置, 直到找到比它小的值.
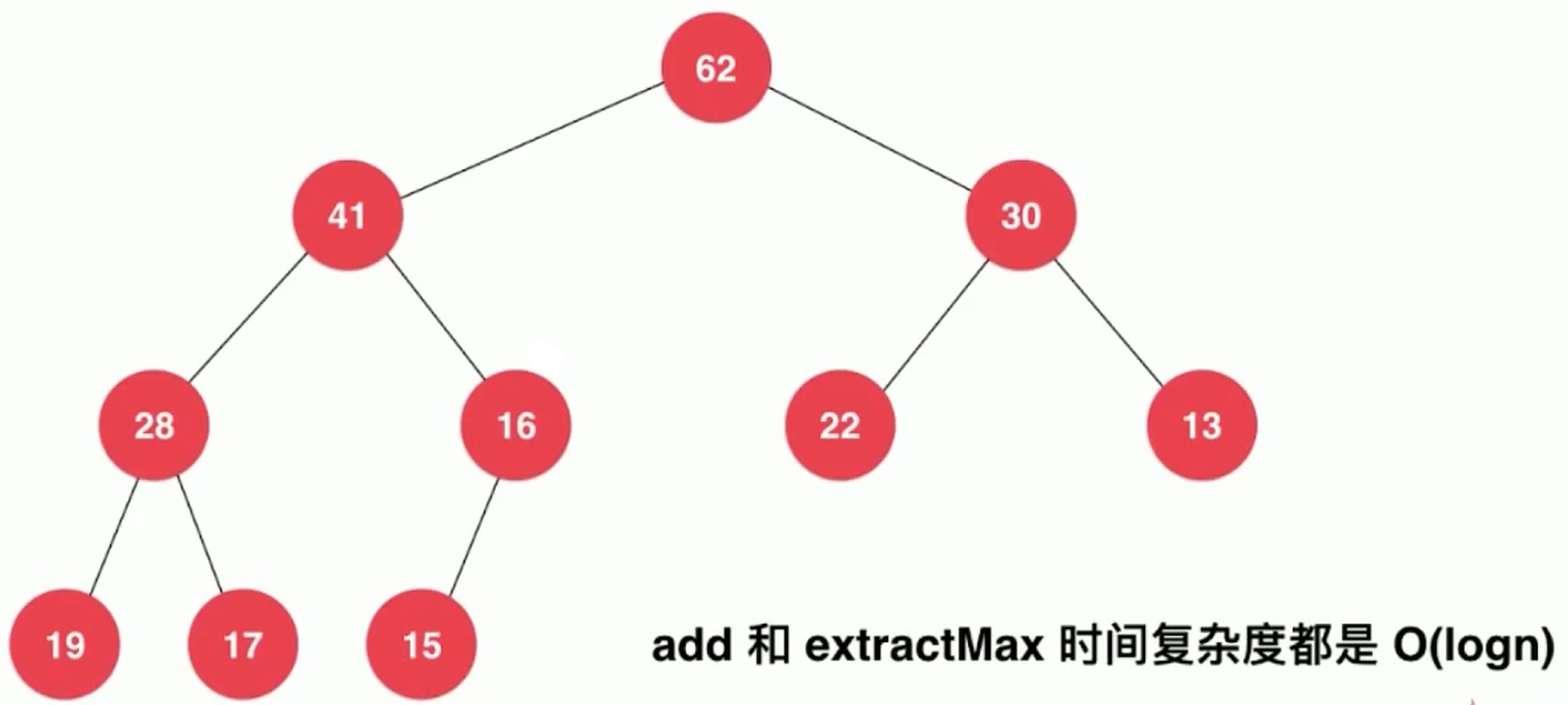
因为是一棵完全二叉树, 所以不会退化成链表, 也就是说不会出现 O(n) 复杂度的情况.
replace: 取出最大元素之后, 再放入一个新元素.
实现1: 先 extractMax, 再add, 两次O(logn)的操作.
实现2: 直接把堆顶元素替换后再 sift down, 一次O(logn)操作.
heapify: 将任意数组整理成堆的形状
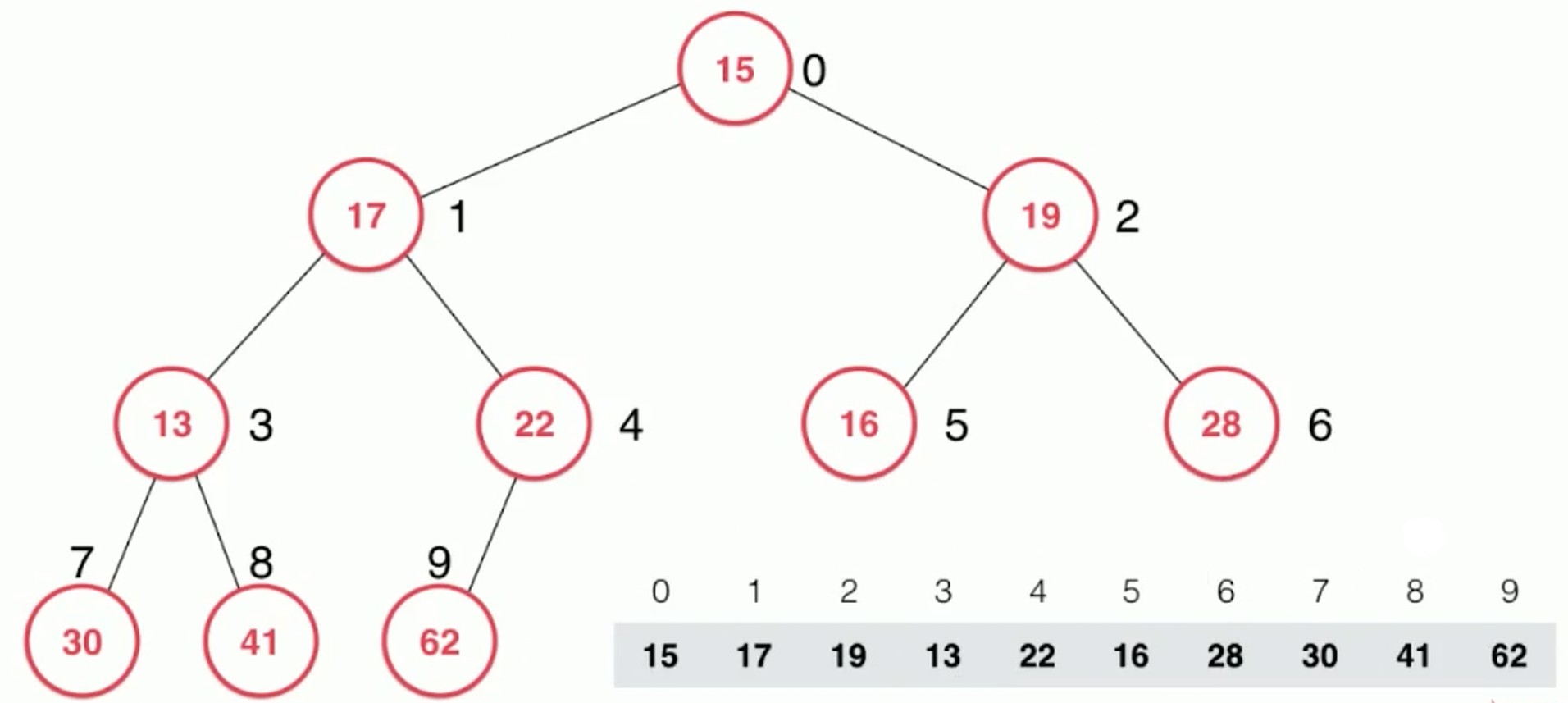
从最后一个非叶子节点开始计算. 上图的话就是22. 然后不断进行下沉操作.
计算最后一个非叶子节点, 最后一个节点的父亲节点就是了.
优先队列
普通队列: 先进先出, 后进后出.
优先队列: 出队顺序和入队顺序无关, 和优先级有关.
动态选择优先级最高的任务执行
Interface Queue<E>
- void enqueue(E)
- E dequeue()
- E getFront()
- int getSize()
- boolean isEmpty()

一般时间复杂度是 logn 的都和树有关.
根据最大堆的特性, 完全可以使用堆来实现优先队列.
优先队列的经典问题
在 1,000,000 个元素选出前100名(在N个元素中选出前M个元素)
排序–NlogN
优先队列–NlogM
可以使用最小堆, 因为要看到前M个最小的元素.
优先级的大小没有说是大的就是优先级高.
二叉堆拓展 – D叉堆 d-ary heap
索引堆, 二项堆, 斐波那契堆
线段树 Segment Tree
线段树 – Segment Tree
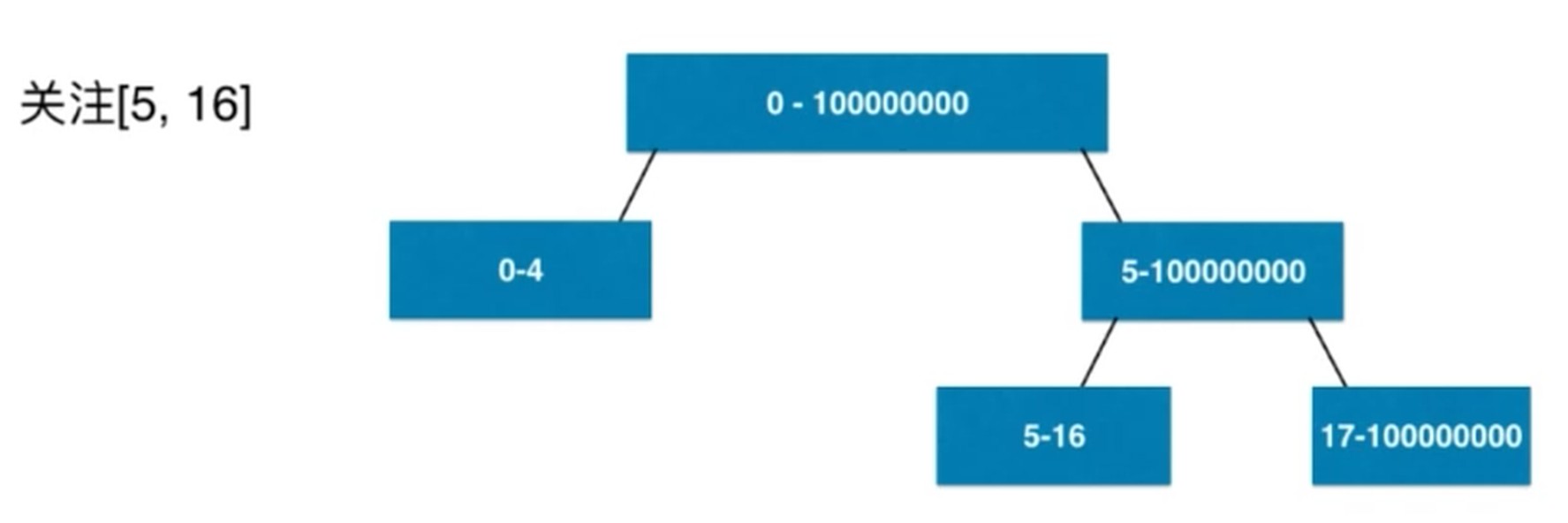
对于一些问题, 需要关心区间.
区间染色, 在[i,j]区间内看见多少种颜色. 使用数组的话, 时间复杂度是O(n), 但是使用线段树的话是O(logn)

另一类经典问题: 区间查询
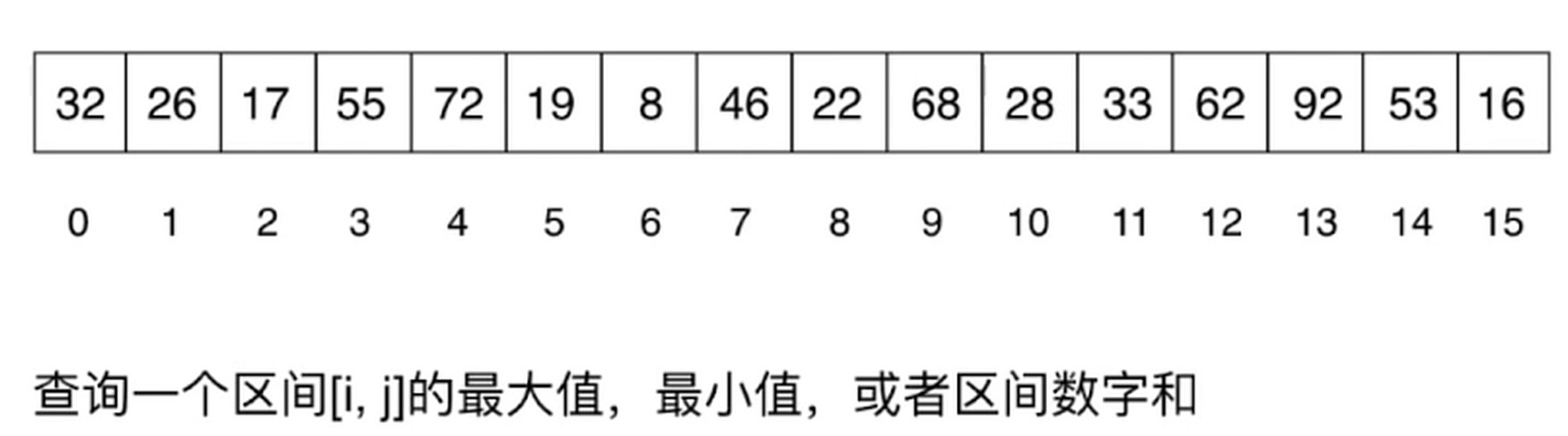
实质: 基于区间的统计查询
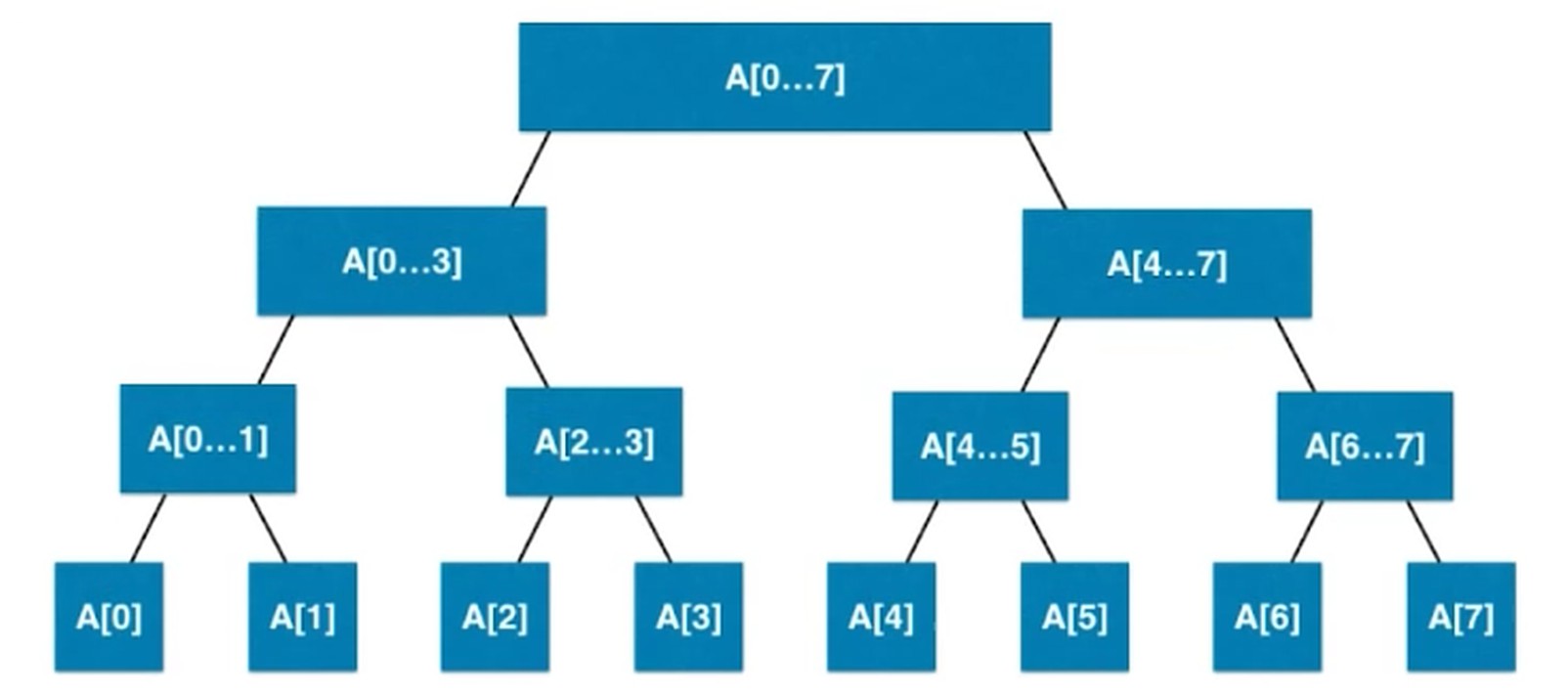
叶子节点不一定都在最后一层, 有可能在倒数第二层
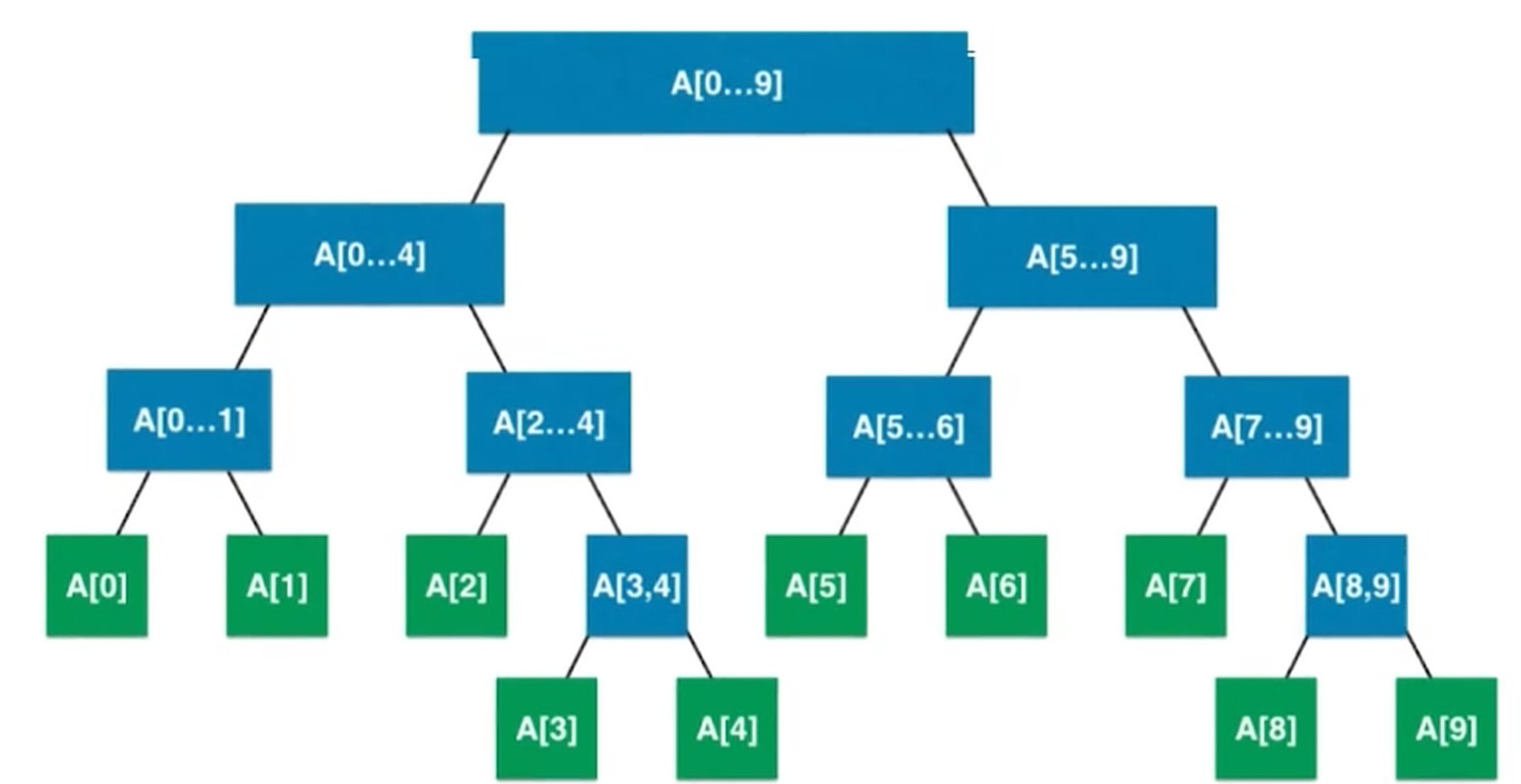
由此可见, 线段树不是完全二叉树.
但是是 平衡二叉树(叶子节点深度相差不超过1, 也就是最大深度和最小深度不超过1, 堆是平衡二叉树, 二分搜索树不是平衡二叉树).
线段树用数组表示, 把它看作是 满二叉树.
对于树, 深度与节点的关系:
h层就有 2^h^ - 1 个节点, h-1层有 2^h-1^个节点, 最后一层的节点树大致等于前面所有层节点之和
所以, 如果区间有 n 个元素, 数组表示需要有多少节点?
如果 n = 2^k^, 只需要 2n 的空间.
最坏情况, 如果 n = 2^k^ + 1, 需要 4n 的空间.
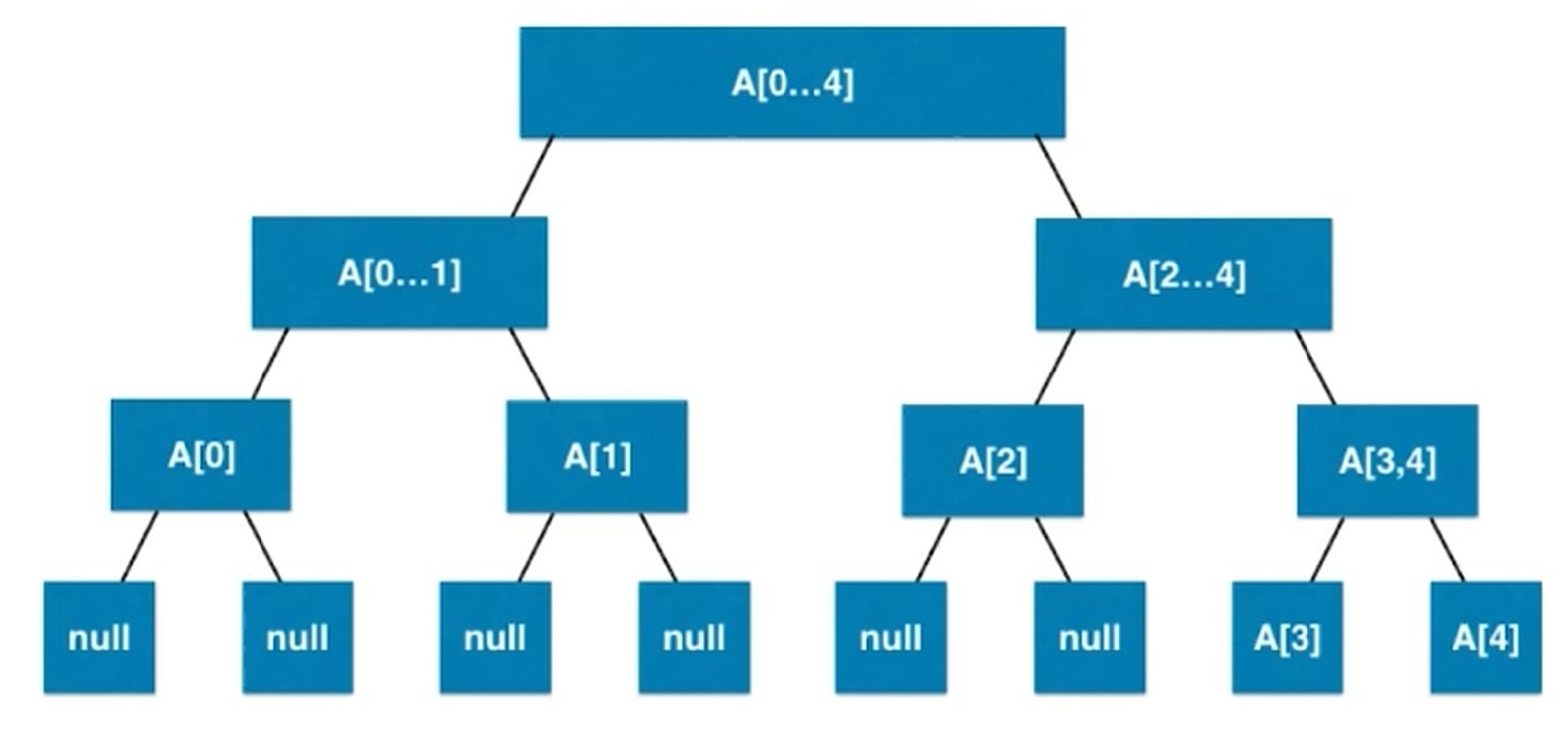
区间查询
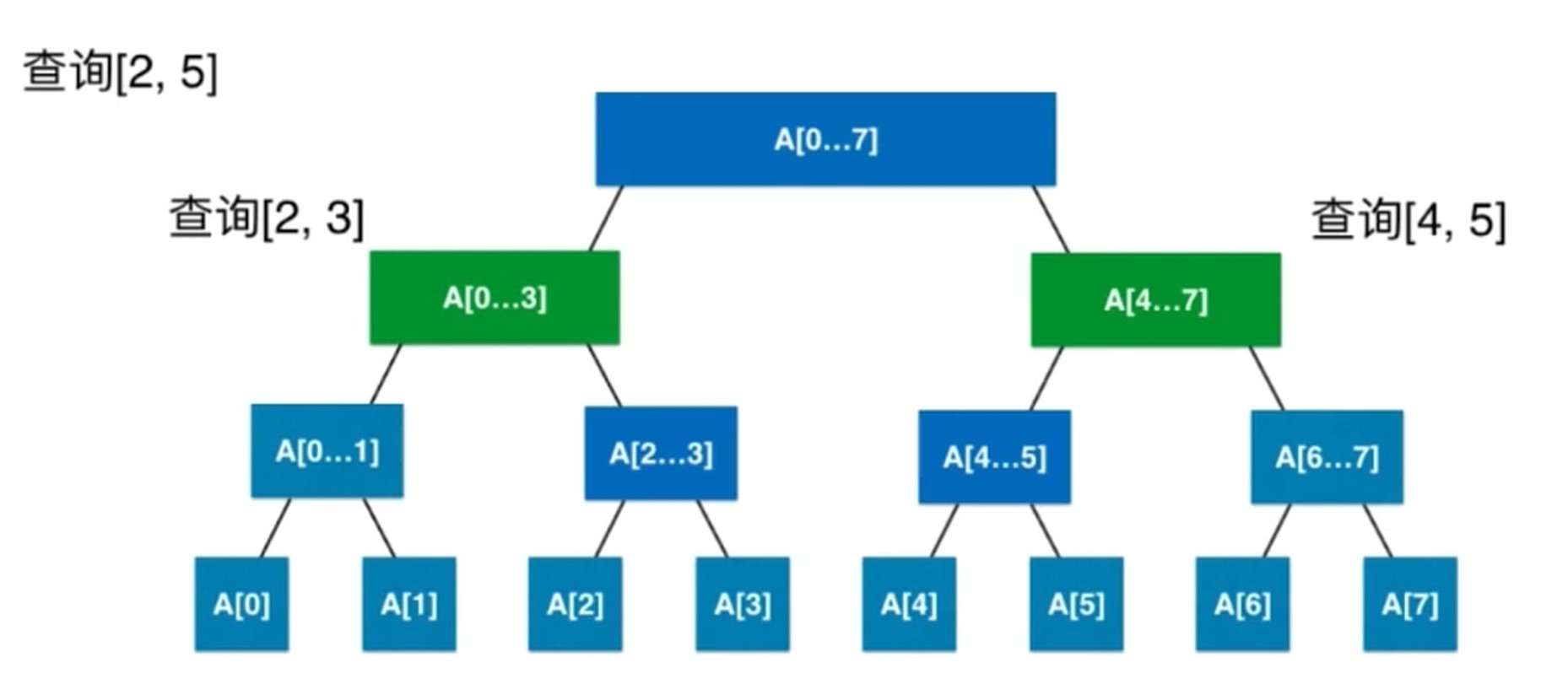
更新区间的话, 注意要把子节点也一起更新了. 这样的话, 就是一个 O(n) 复杂度的操作了.
解决方案: 懒惰更新. 使用 lazy 数组记录未更新的内容. 在查询到这些节点的时候再更新.
线段树扩展
二维线段树, 一维线段树, 就是节点处理的数据是在一个一维空间的.
动态线段树. 使用链表的形式.
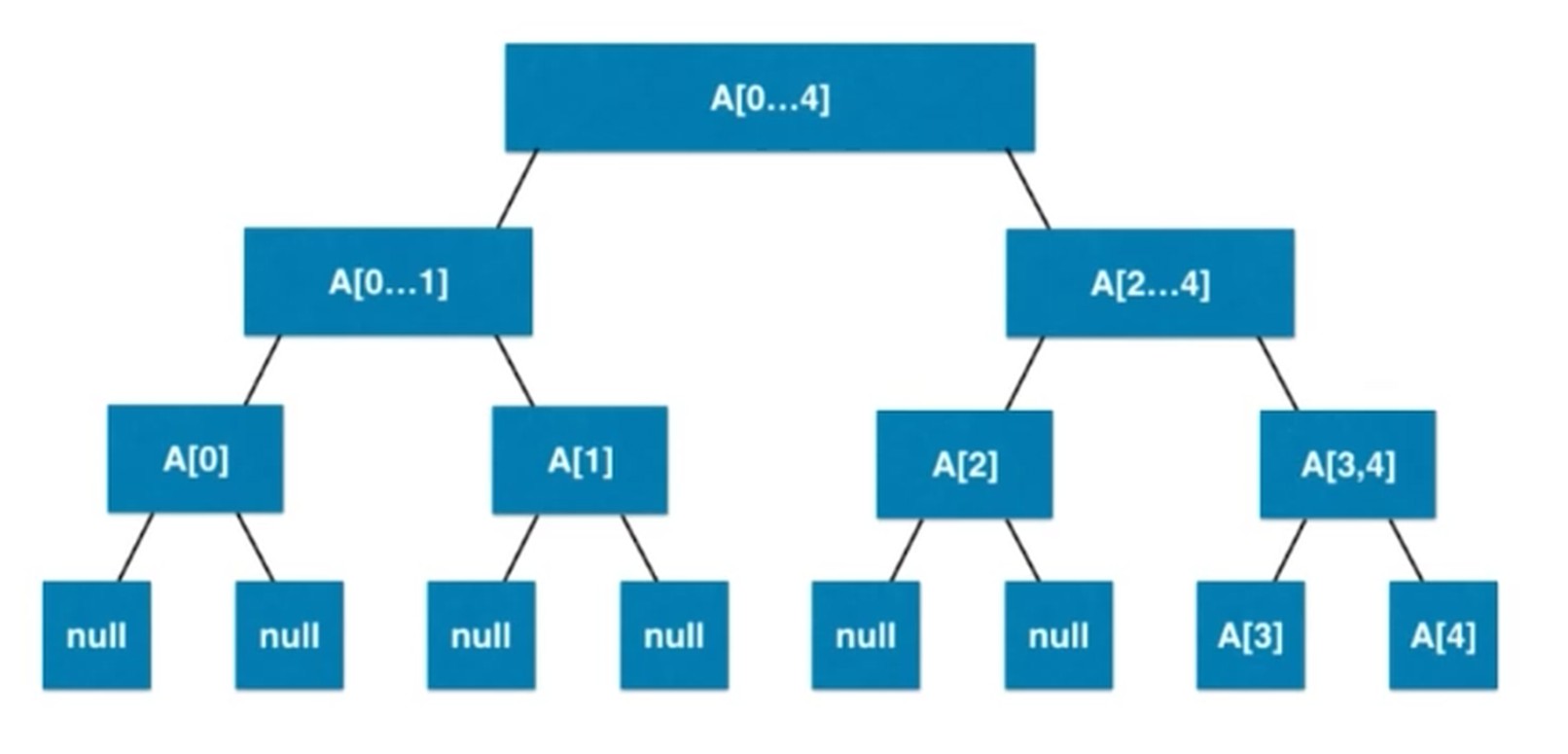
需要关注的时候再动态划分
区间操作相关的另外一个重要数据结构
树状数组, Binary Index Tree
字典树 Trie
字典树也称作前缀树, 属于多叉树.
查询每个条目的时间复杂度, 和字典中的条目数无关. 跟要查询字符串的长度相关.
时间复杂度为 O(w), w是查询字符串的长度.
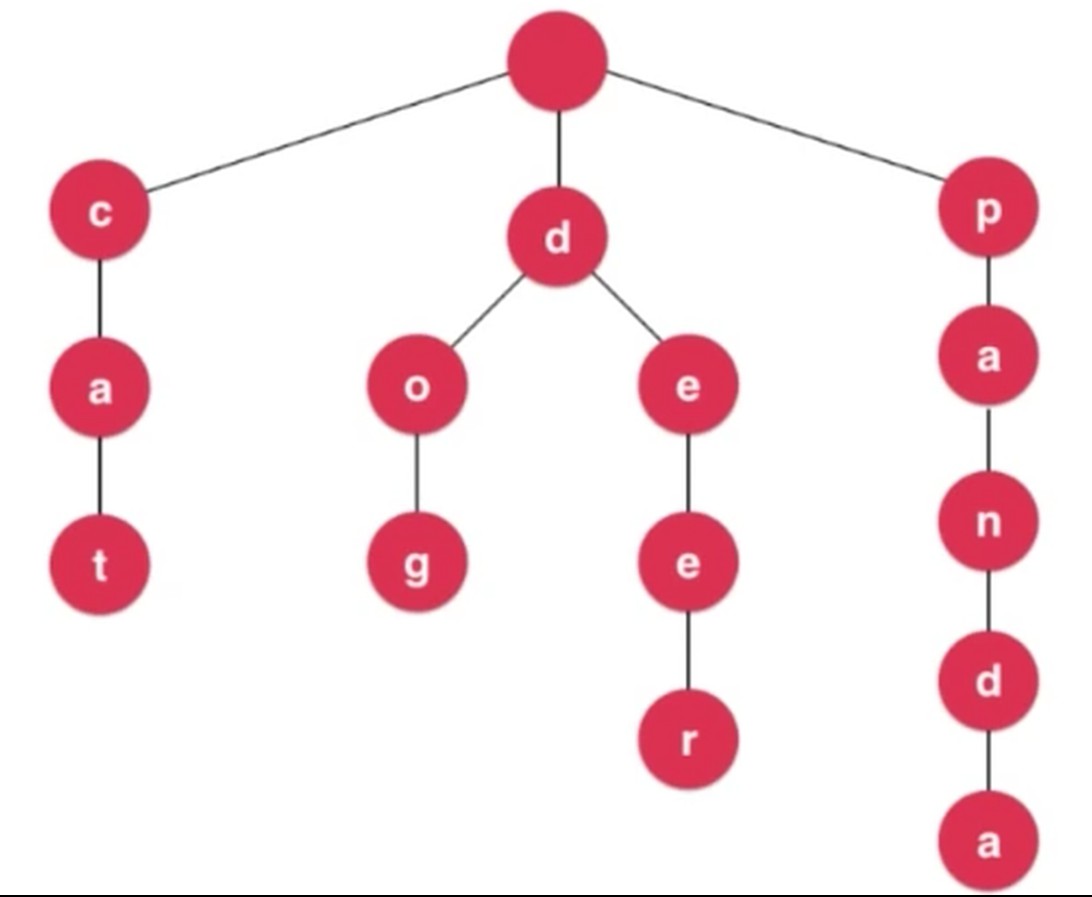
每个节点都有26个指向下一个节点的指针.
// Trie 节点的结构
class Node{
char c;
Node next[26];
}
考虑不同的语言, 不同的情景
每个节点有若干个指向下一个节点的指针.
class Node{
char c;
// 如果是26个字符的话, 占用空间是原来的27倍了
// 每个字符映射到一个新的节点
Map<char, Node> next;
}
实际, 来到节点之前, 就知道字母是什么了, 所以应该在边上, 每个节点就可以不存储 char c 了. 下图蓝色代表 叶子节点.
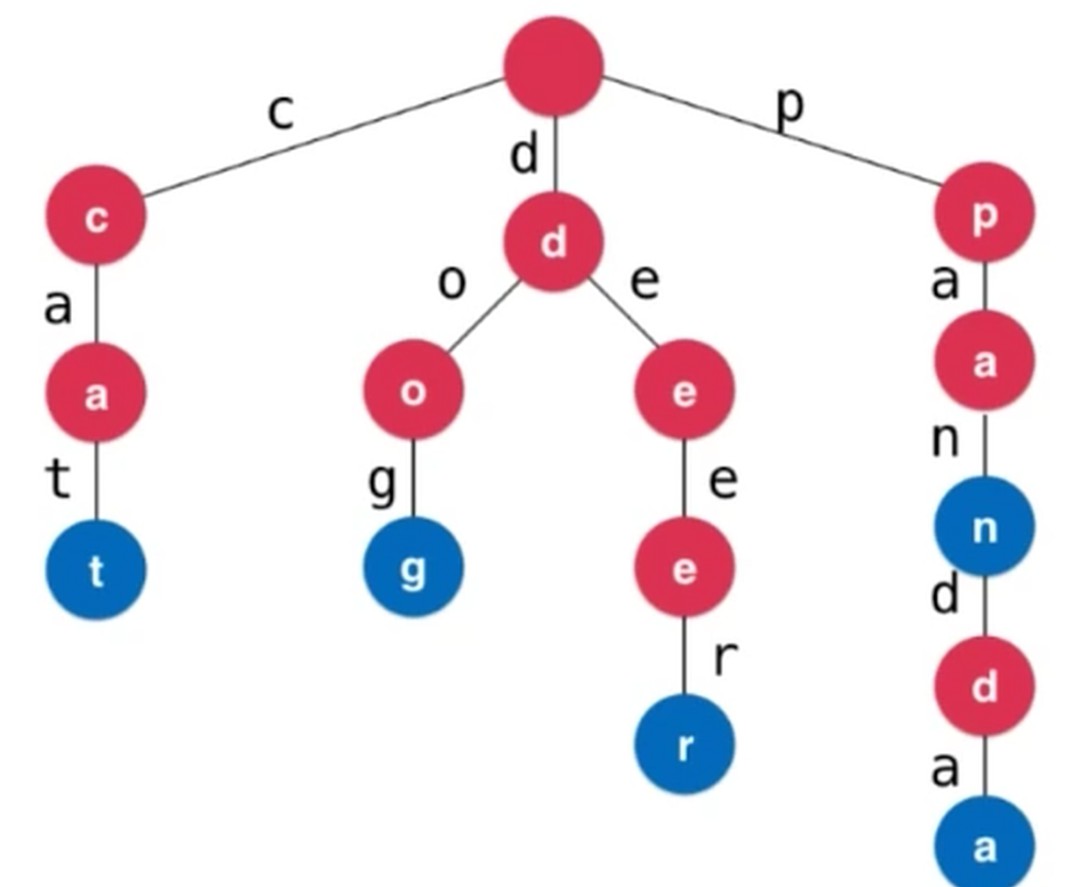
class Node{
// 是否是单词的结尾
boolean isWord;
Map<char, Node> map;
}
字典树扩展
前缀搜索
模式匹配
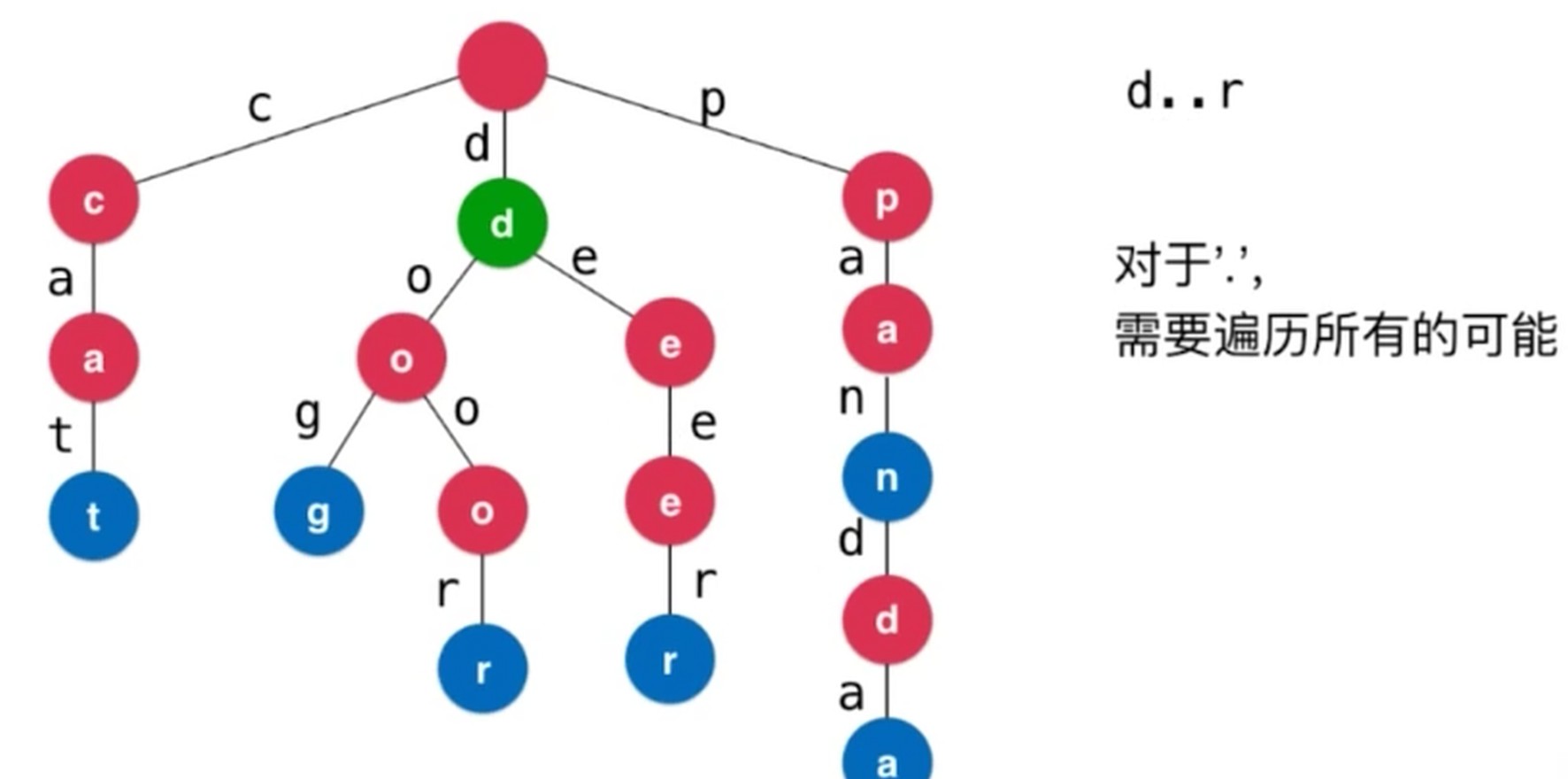
删除操作
Trie局限性, 空间占用大.
压缩字典树 Compressed Trie, 缺点是维护成本更高了.
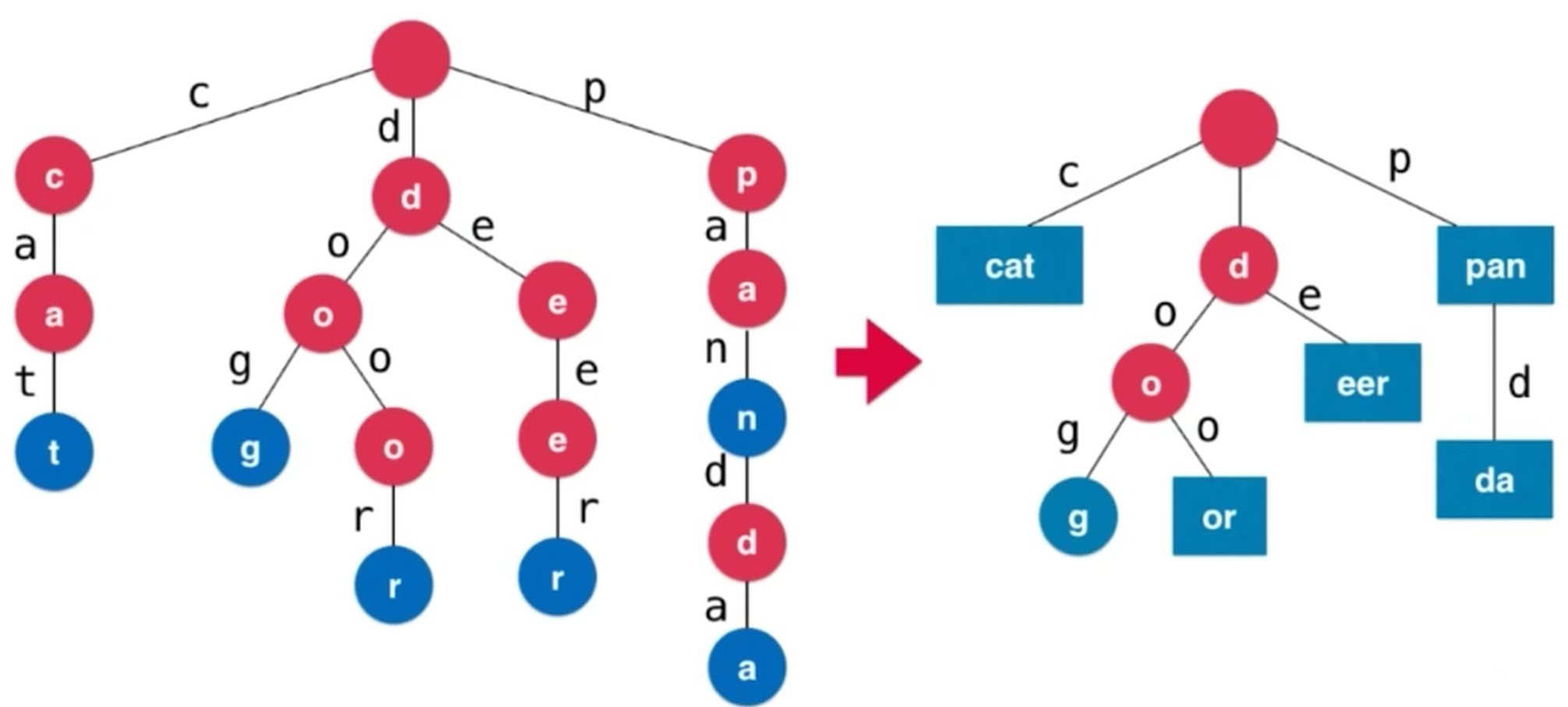
三分搜索树, Ternary Search Trie
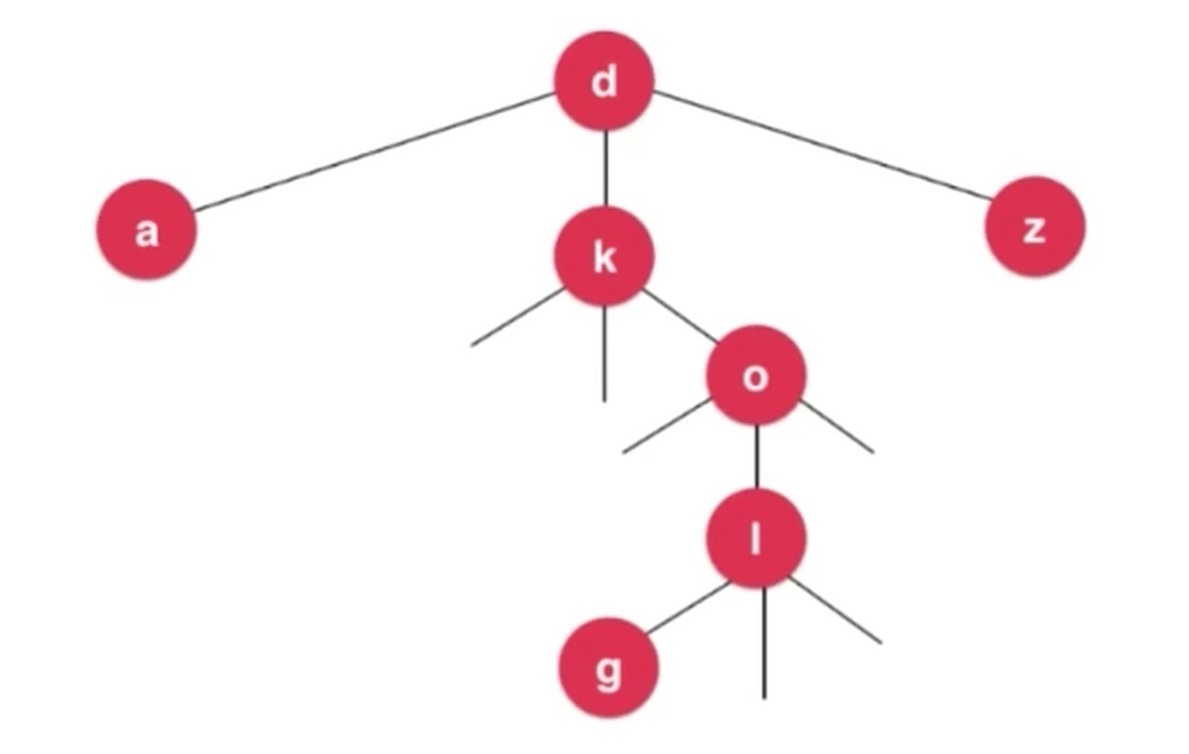
后缀树
子串查询, 一个字符串是否是另外一个字符串的子串, 例如文本搜索
- KMP
- Boyer-Moore
- Rabin-Karp
文件压缩, 模式匹配, 编译原理
并查集 Union Find
一般都是父亲指向孩子的, 而并查集是孩子指向父亲的.
并查集可以很快地查询到 网络中节点间的连接状态.
- 网络是一个抽象的概念: 用户之间形成的网络
数学中的集合类实现
连接问题 和 路径问题
连接问题其实是比路径问题要回答的问题少的, 连接是 是或否 的问题, 而路径是一个具体线路的问题.
如果连接问题用路径问题来回答, 明显是消耗了没必要的资源.
- 和堆做比较
两个操作
- union(p, q)
- isConnected(p, q)
QuickFind
使用数组进行模拟.
数据表示如下图, 10个元素, 分在0和1这2个集合之中. 在同一个集合的可以连接.
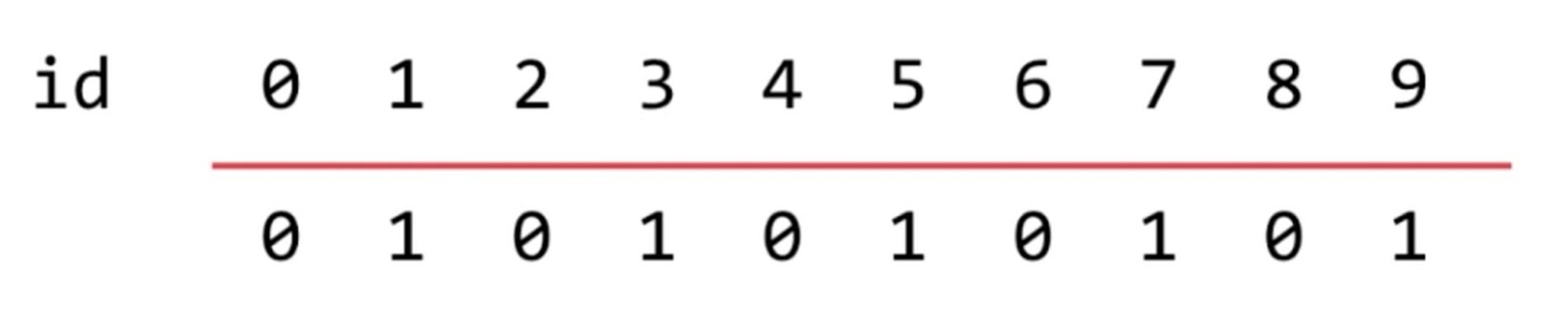
isConnected(p, q) -> find(p) == find(q)
而 Quick Find 时间复杂度 O(1)
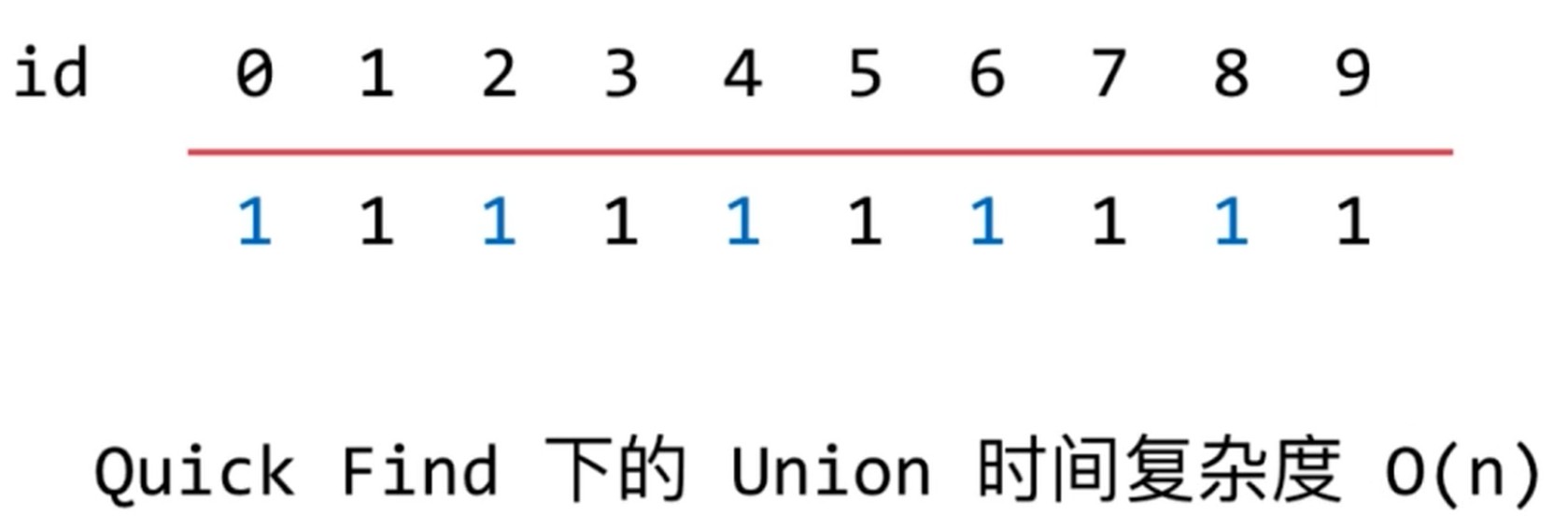
如果是Union, 时间复杂度就变成 O(n) 了
QuickUnion
将每个元素, 看作是一个节点. 要让 7 和 2 连接, 只要 2 和 5 连接即可.
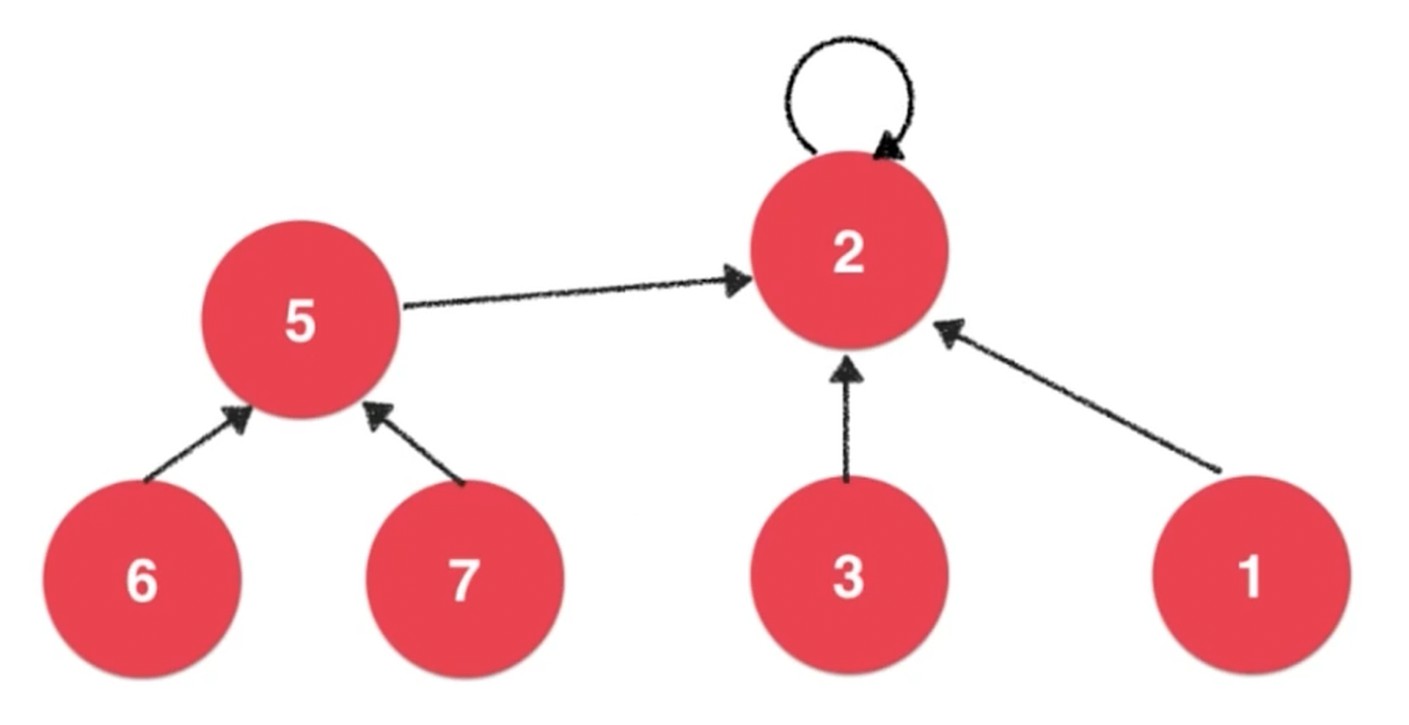
parent[i] 就是第i个元素所在节点指向的元素.
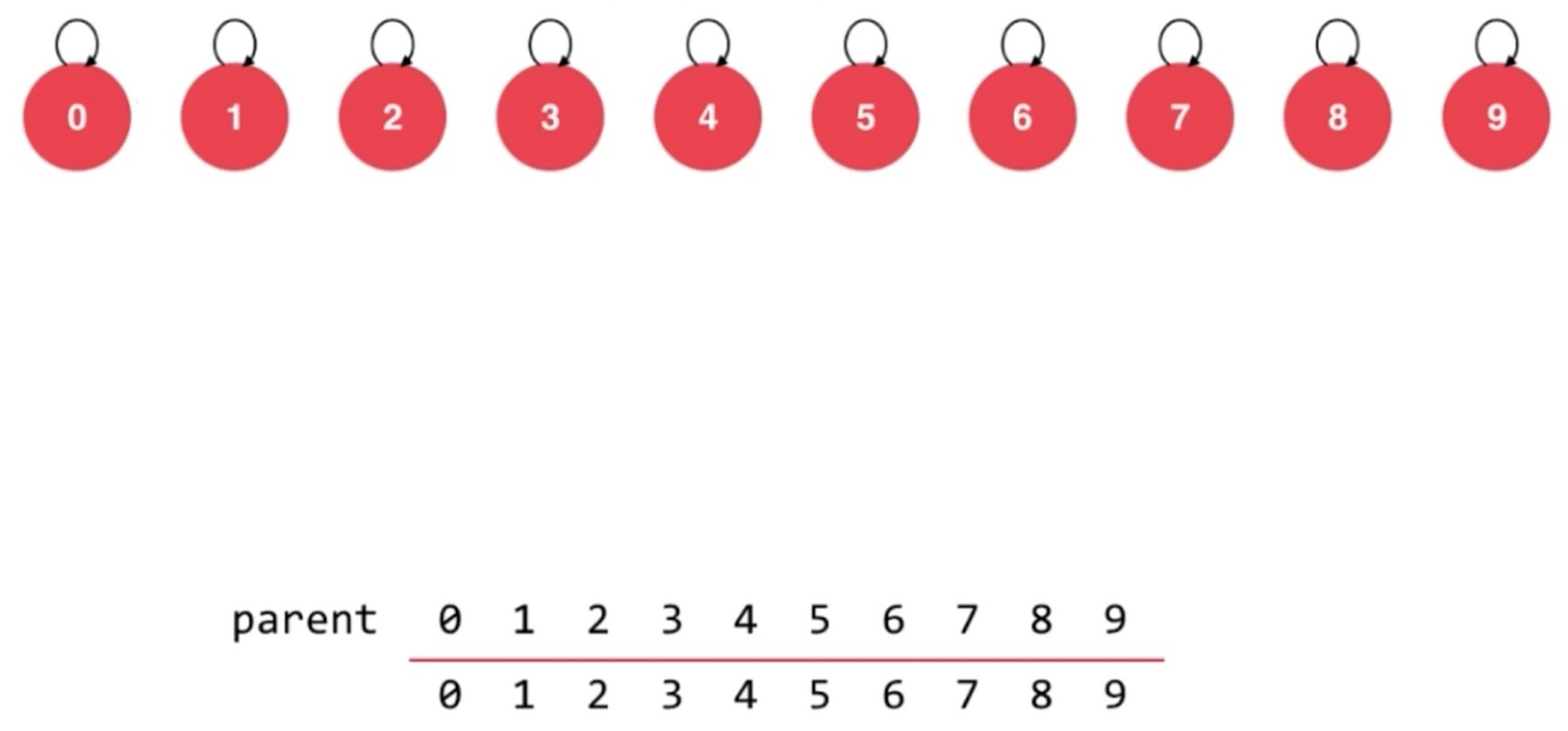
操作 Union 4, 3
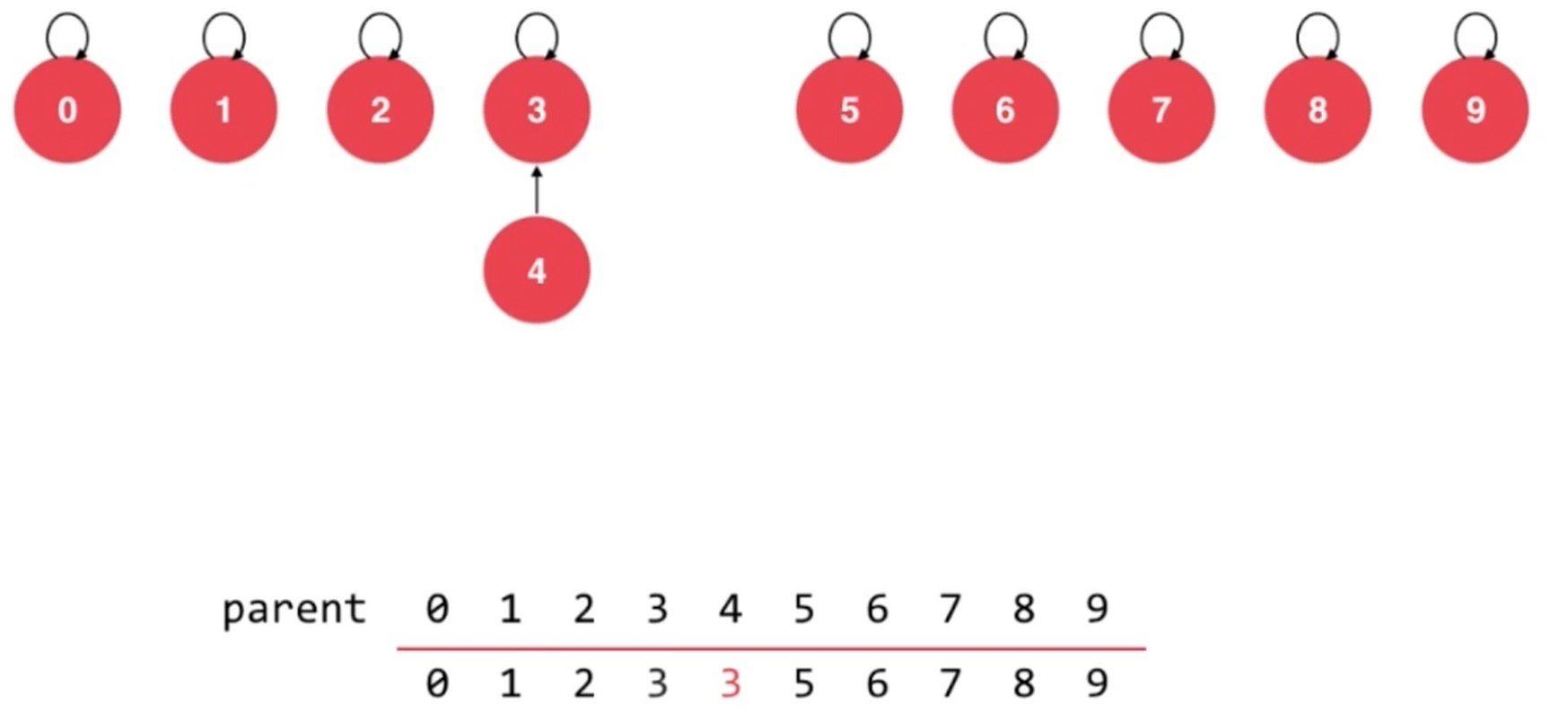
操作 Union 6, 2
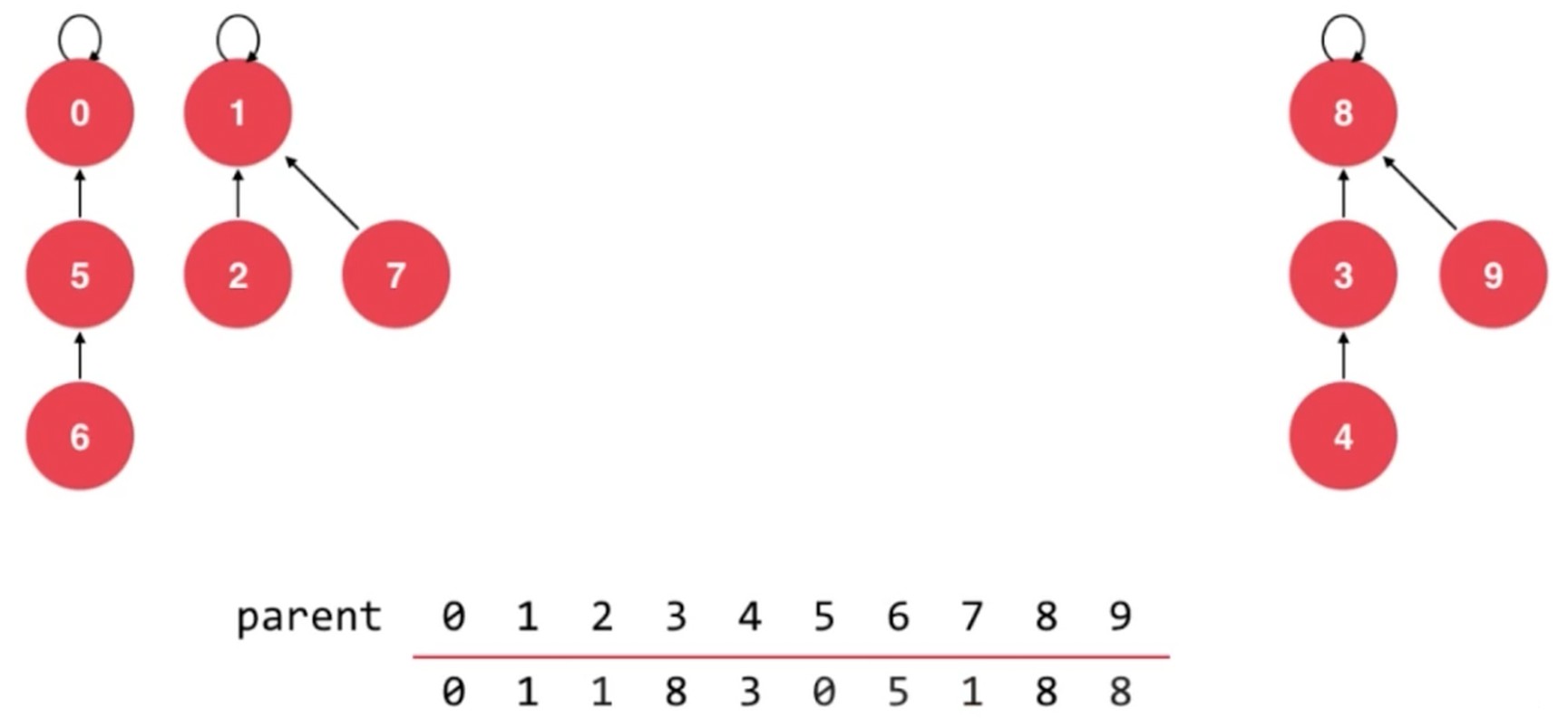
让 0 指向 1 即可
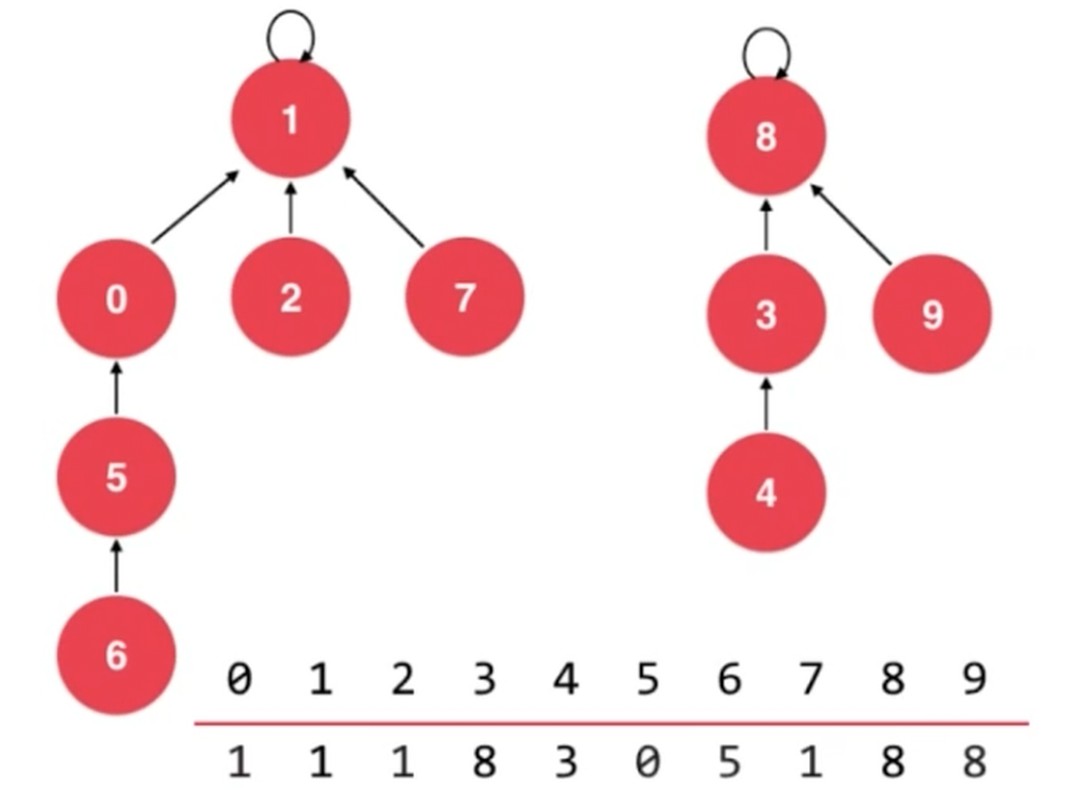
基于 size 优化, 基于 rank 优化.
rank优化例子
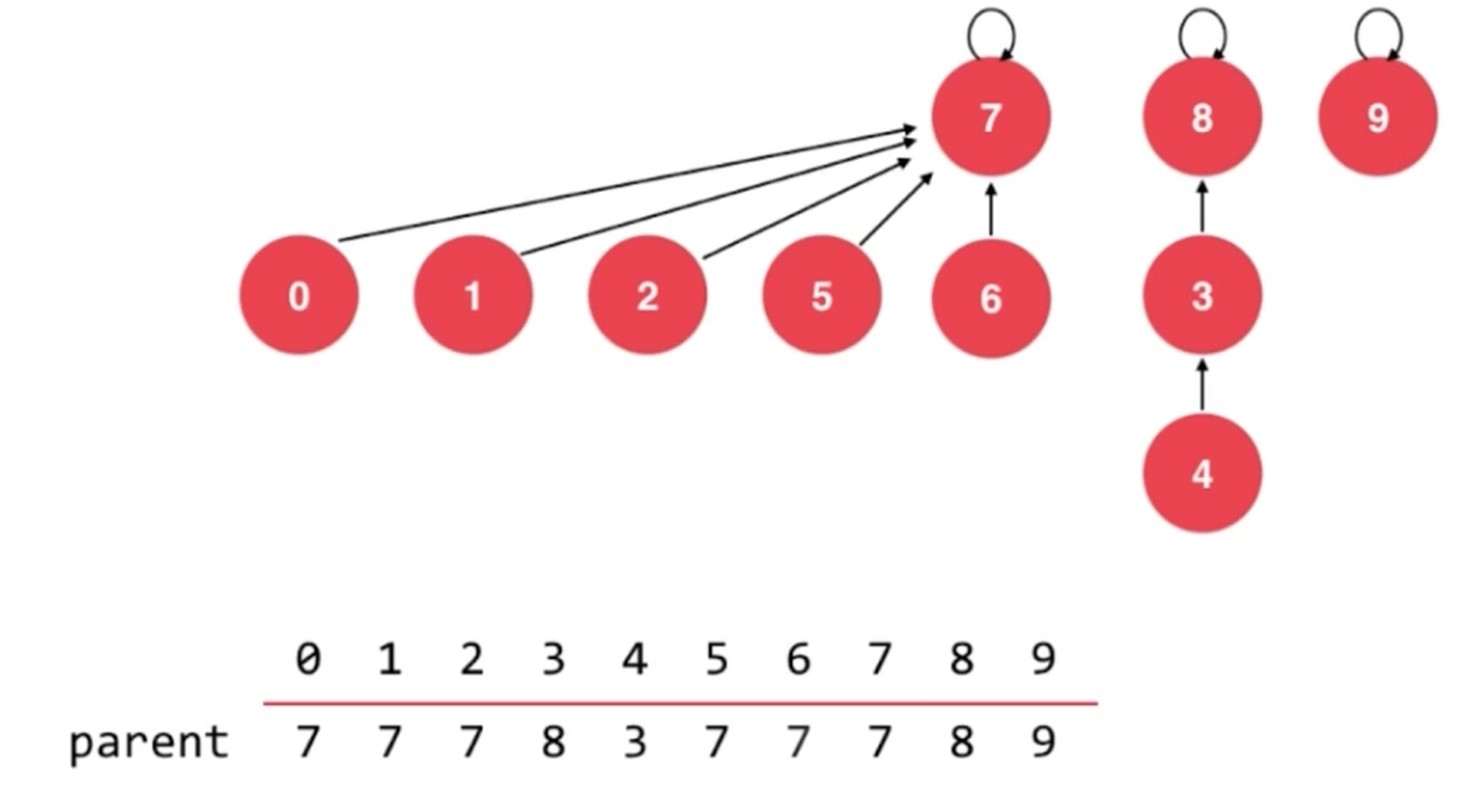
如果合并到节点总数大的节点上. 合并后, 树的深度增加到4了. 明显是不太合理的.
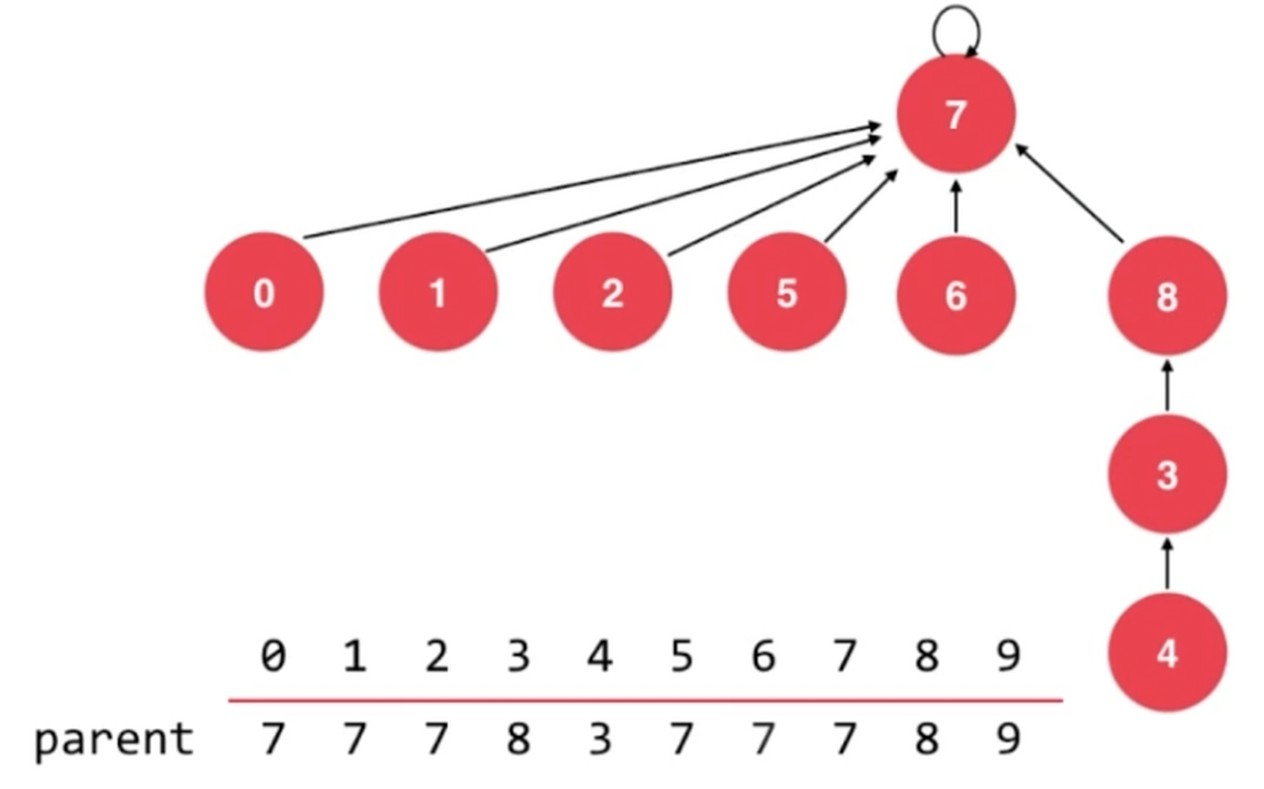
如果是深度低的合并到深度高的节点上, 深度没有改变, 这样就更加合理.
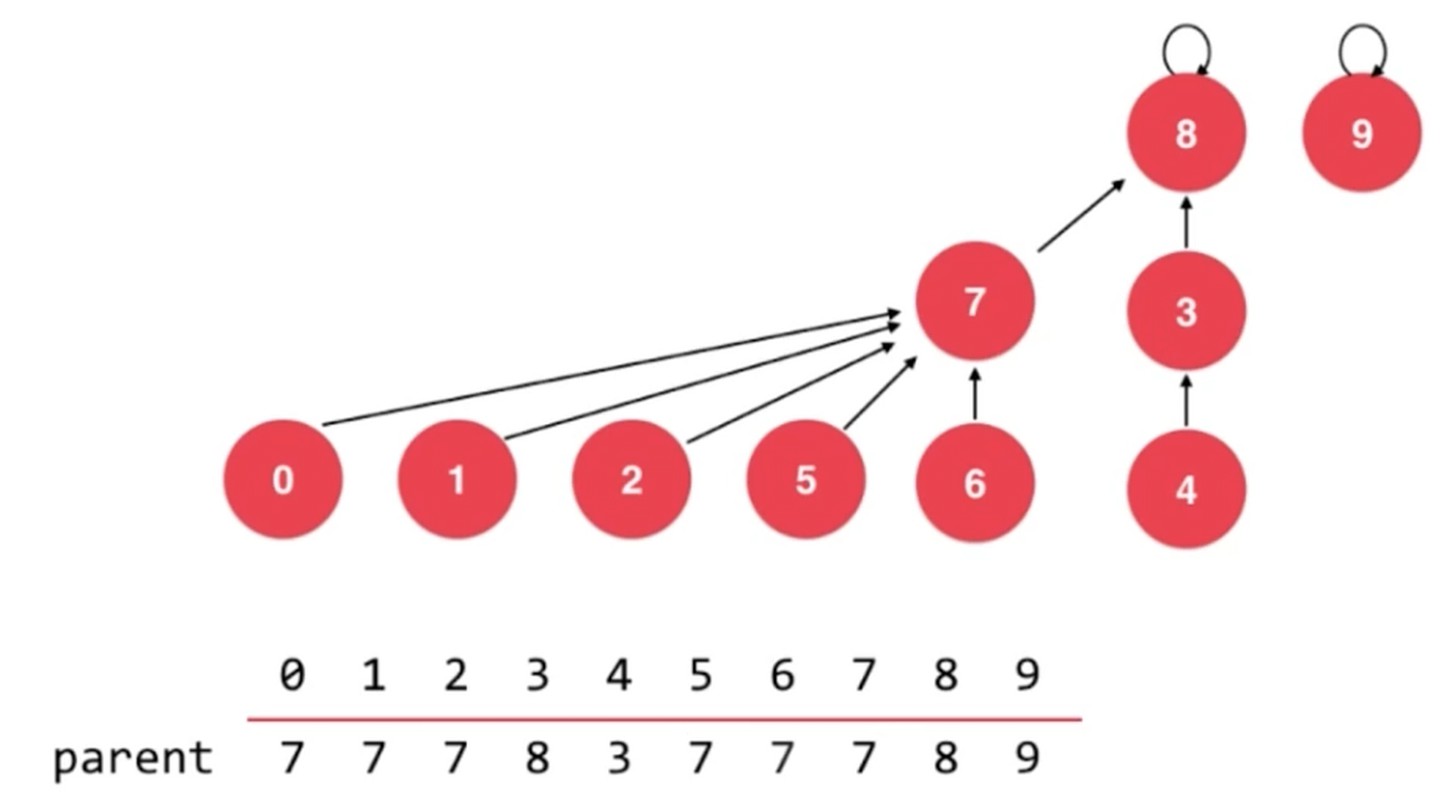
以上就是 rank优化, rank[i]表示根节点为i的树的高度.
路径压缩优化, 就是降低树的高度.
下图虽然都是表示同一种集合, 但是效率是不一样的
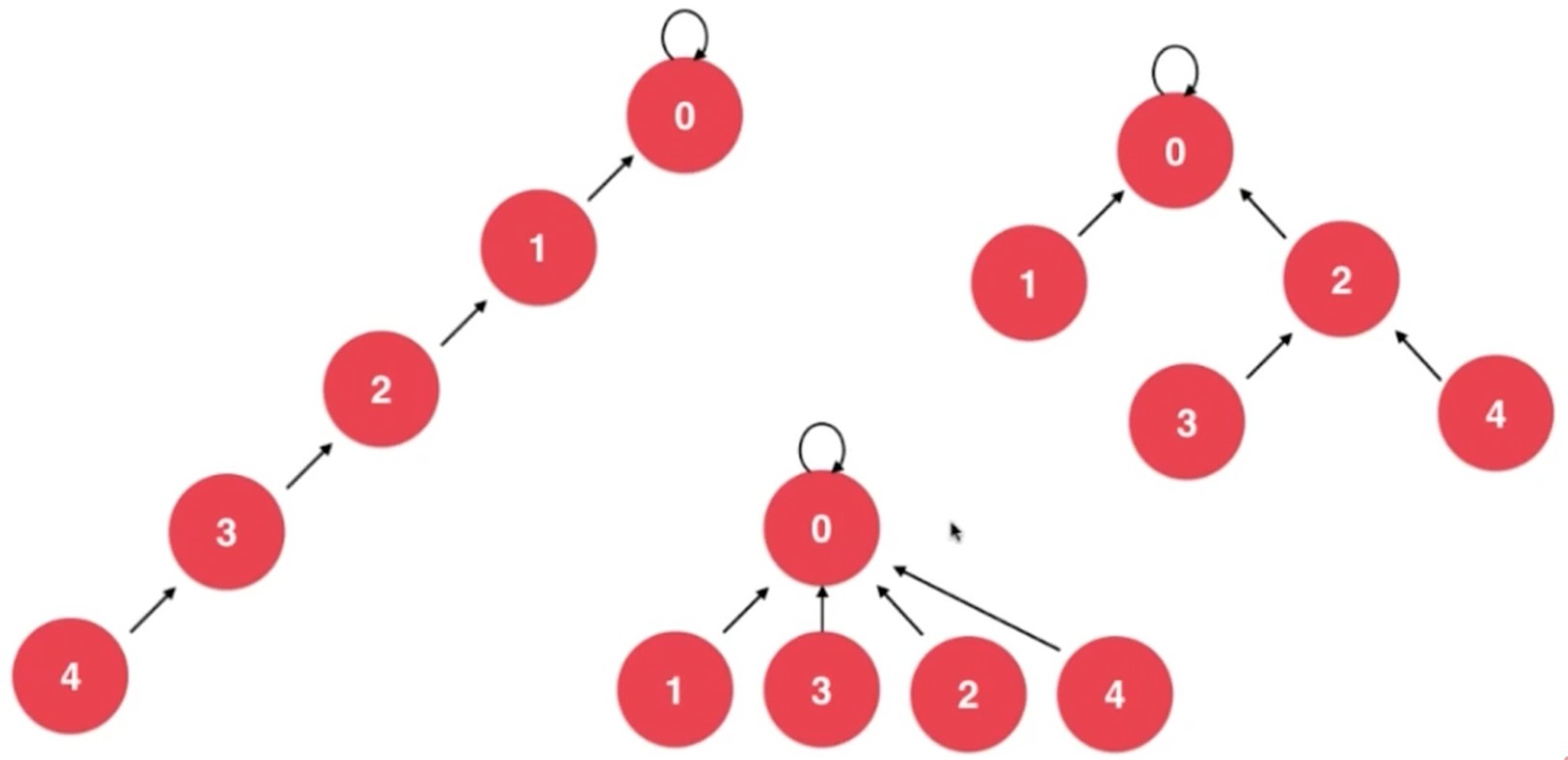
路径压缩例子
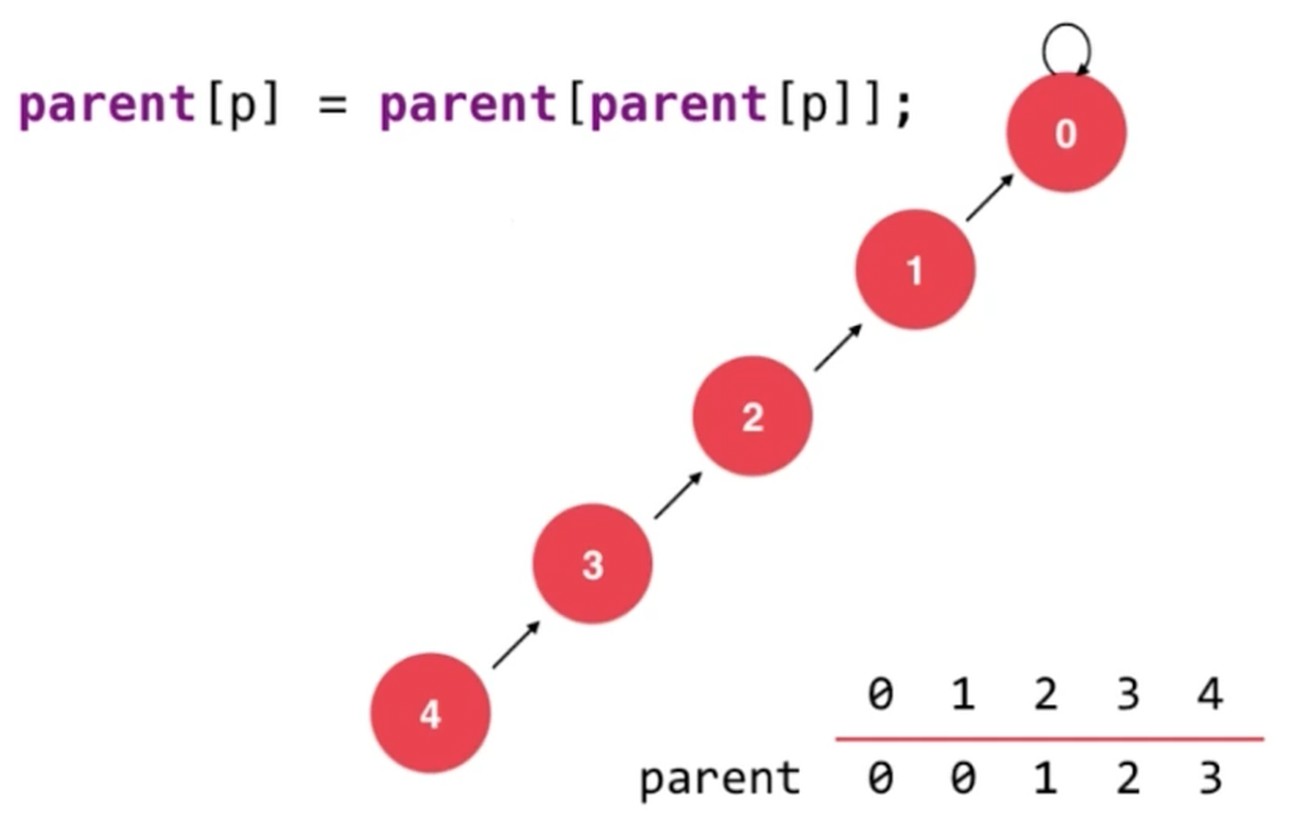
将p节点设置为父亲的父亲, parent[p] = parent[parentp[p]], 执行这句话之后如下图
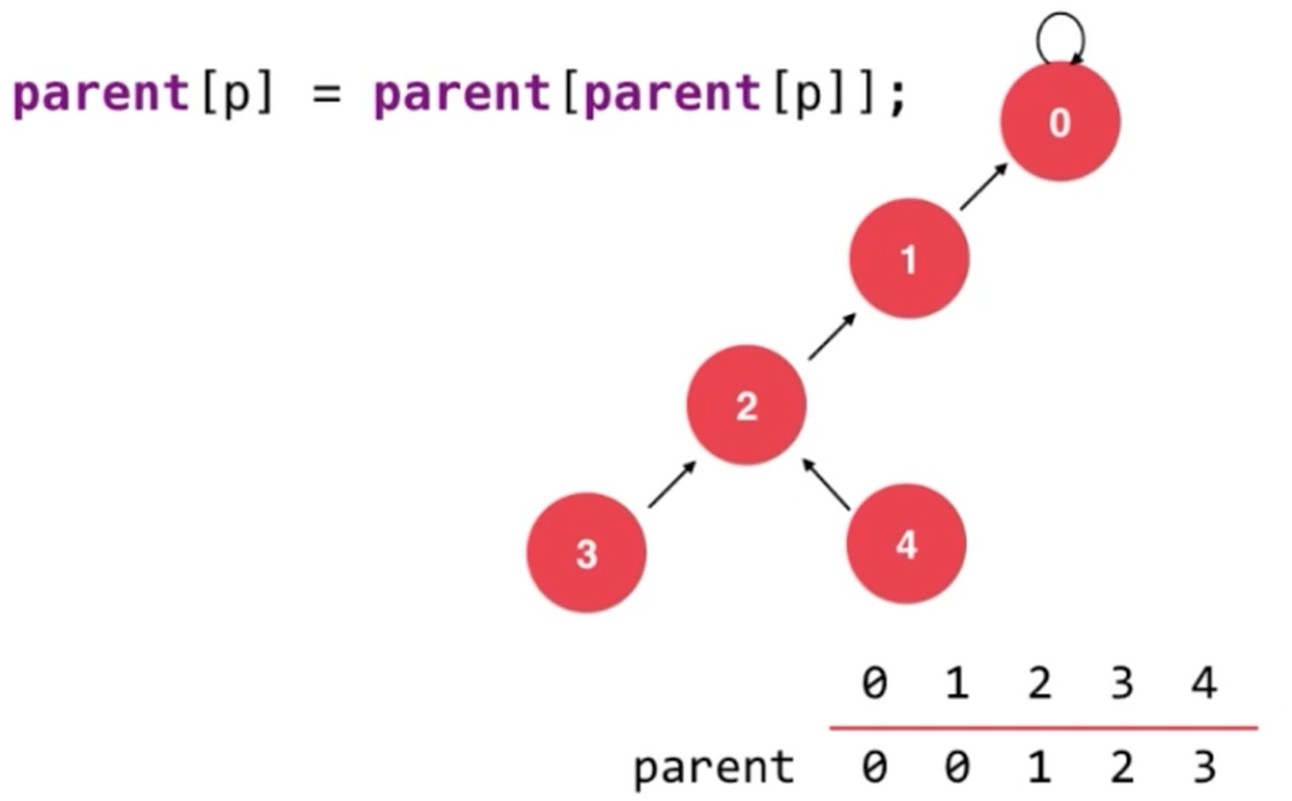
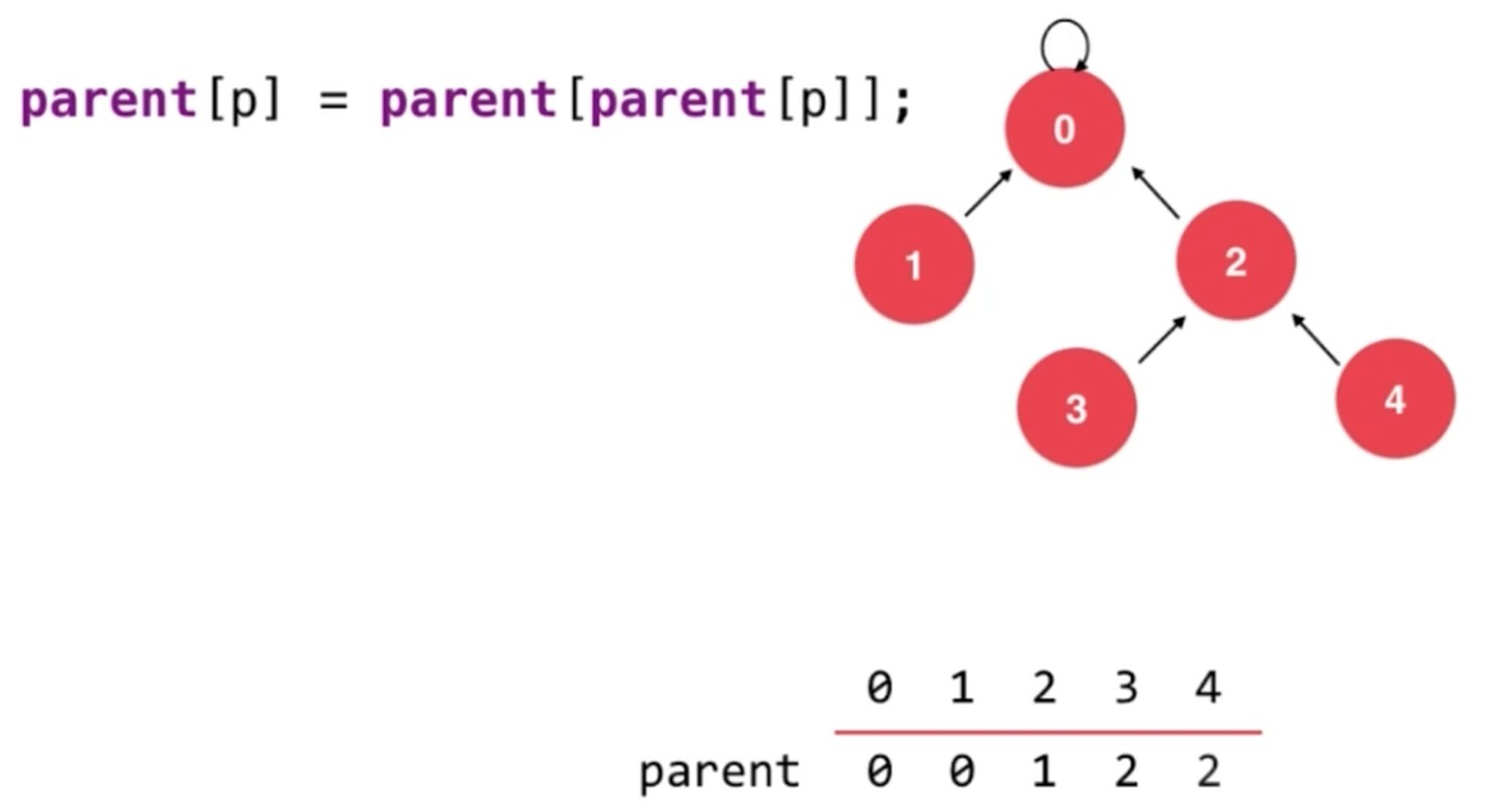
时间复杂度分析
O(h)

上面的复杂度, 近乎是O(1)级别的.
平衡二叉树 AVL
发明人的名字缩写. G.M. Adelson-Velsky 和 E.M. Landis.
最早的自平衡二分搜索树结构
线段树是平衡二叉树, 但不是完全二叉树, 满二叉树(没有节点的地方填补空节点)也是平衡二叉树, 叶子节点都不超过一.
定义: 对于任意个节点, 左子树和右子树的高度不能超过1, 相对宽松.
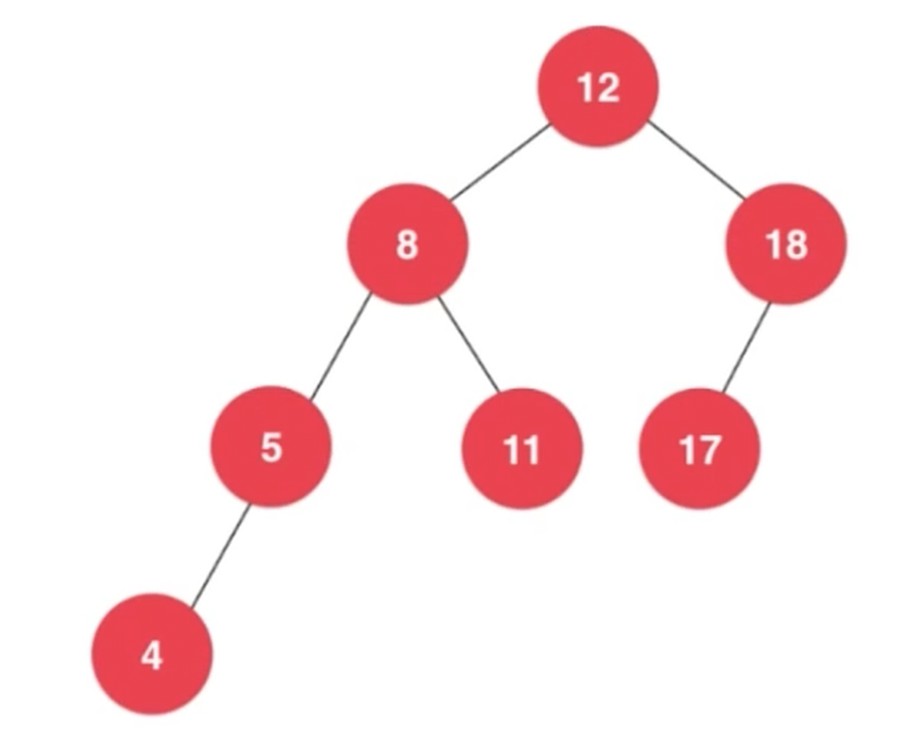
平衡二叉树的高度和节点数量之间的关系也是O(logn)的.
标注节点的高度
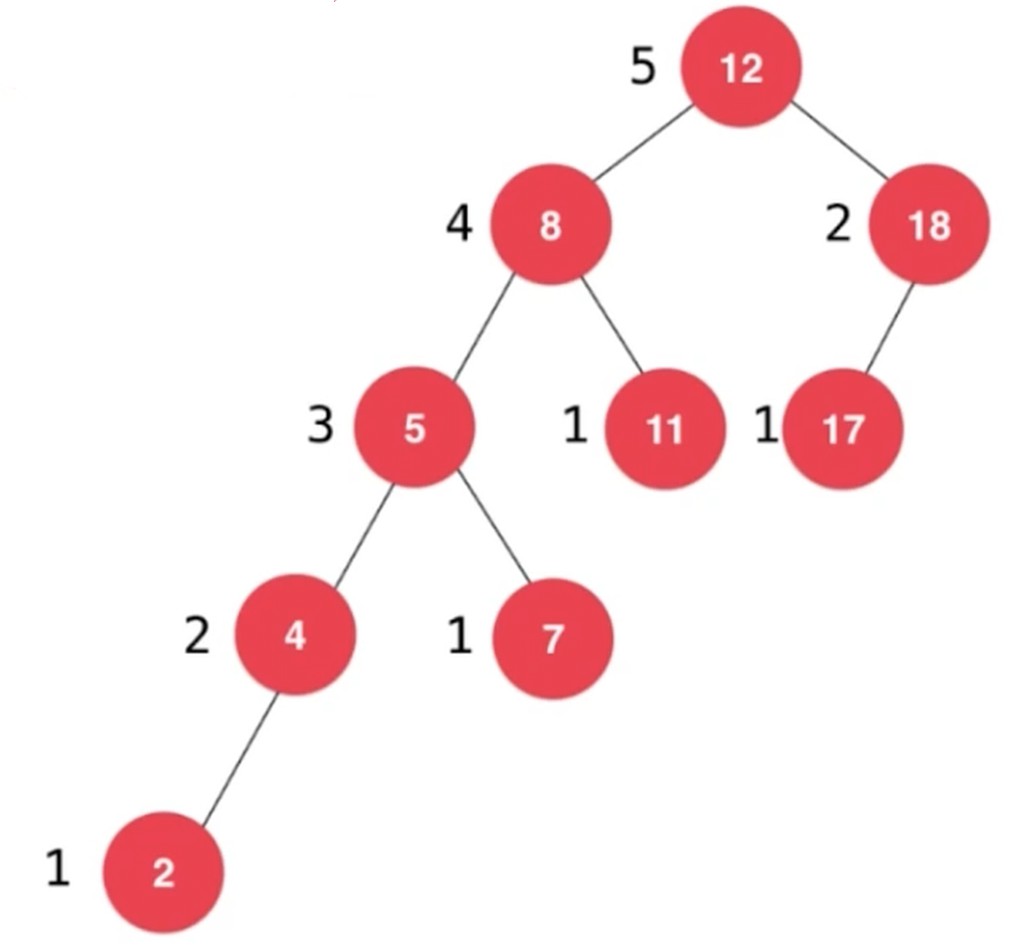
计算平衡因子
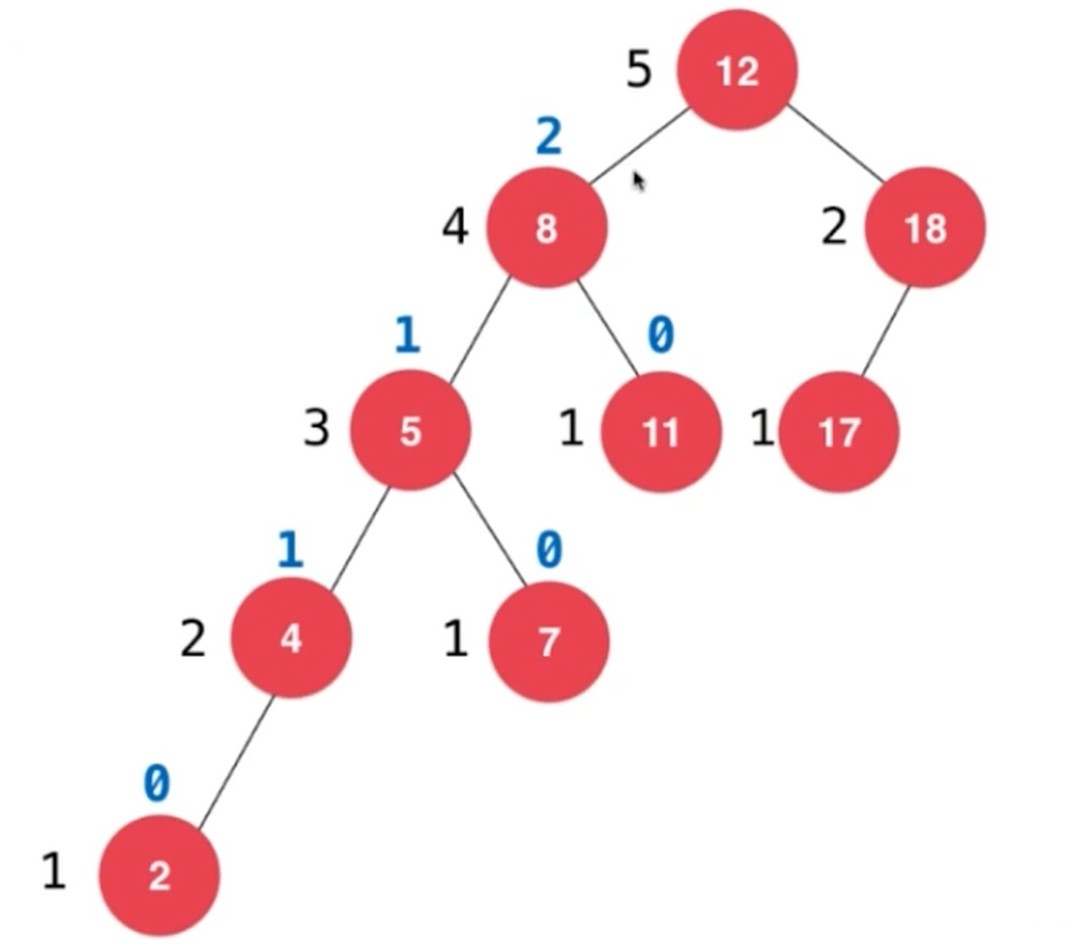
左旋转和右旋转
插入新节点破坏了平衡性, 所以应该在插入的路径上查找原因.
也就是 加入节点后, 沿着节点向上回溯维护平衡性.
右旋转, 插入元素在不平衡节点的左侧的左侧
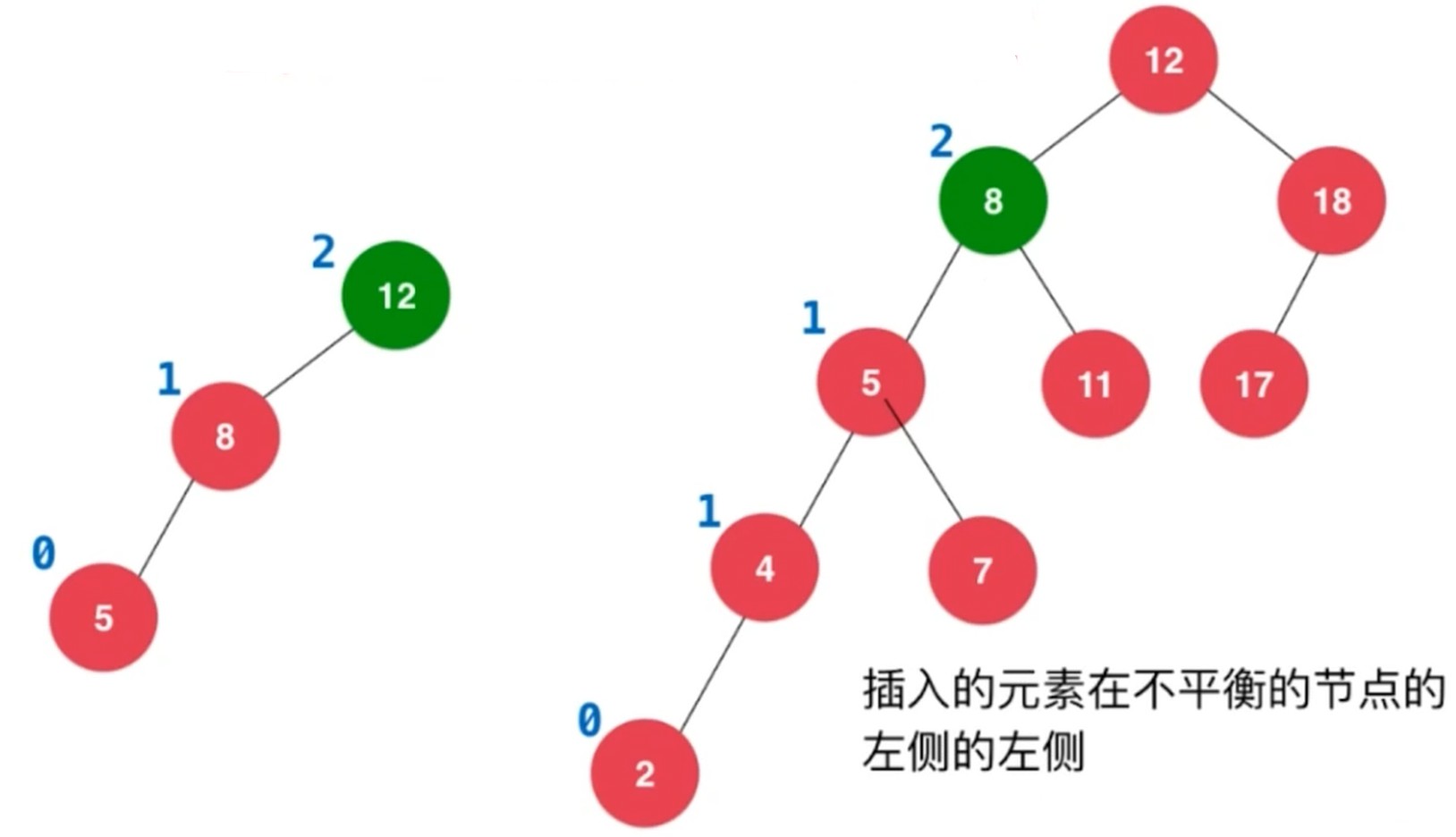
旋转过程
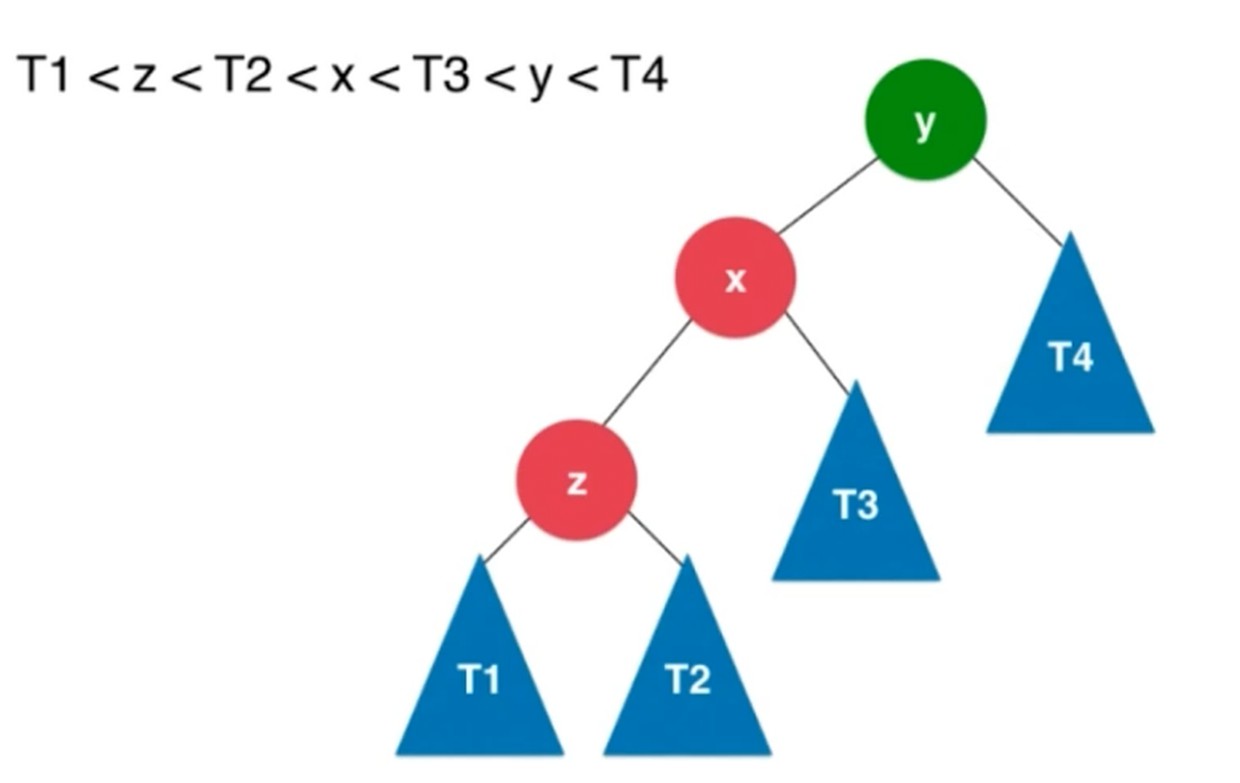
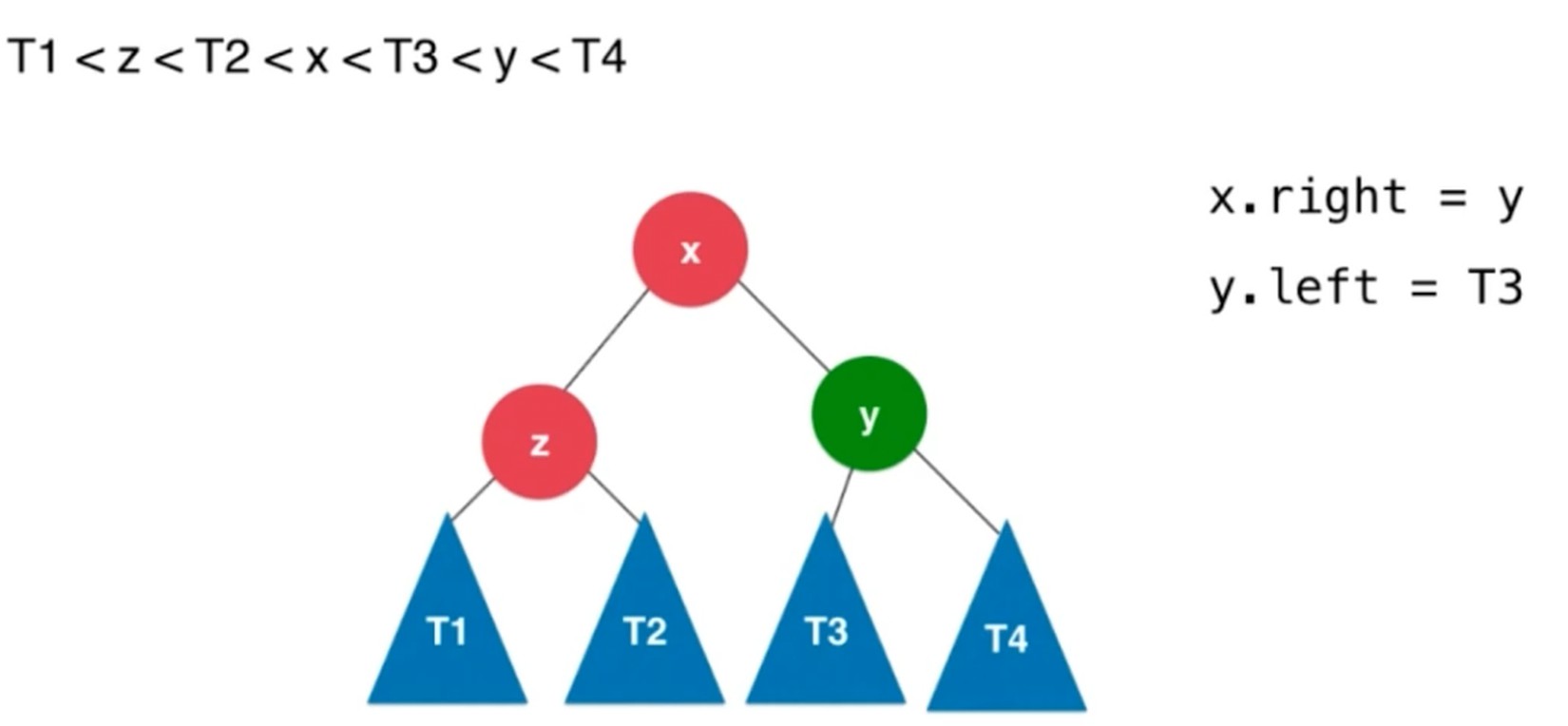
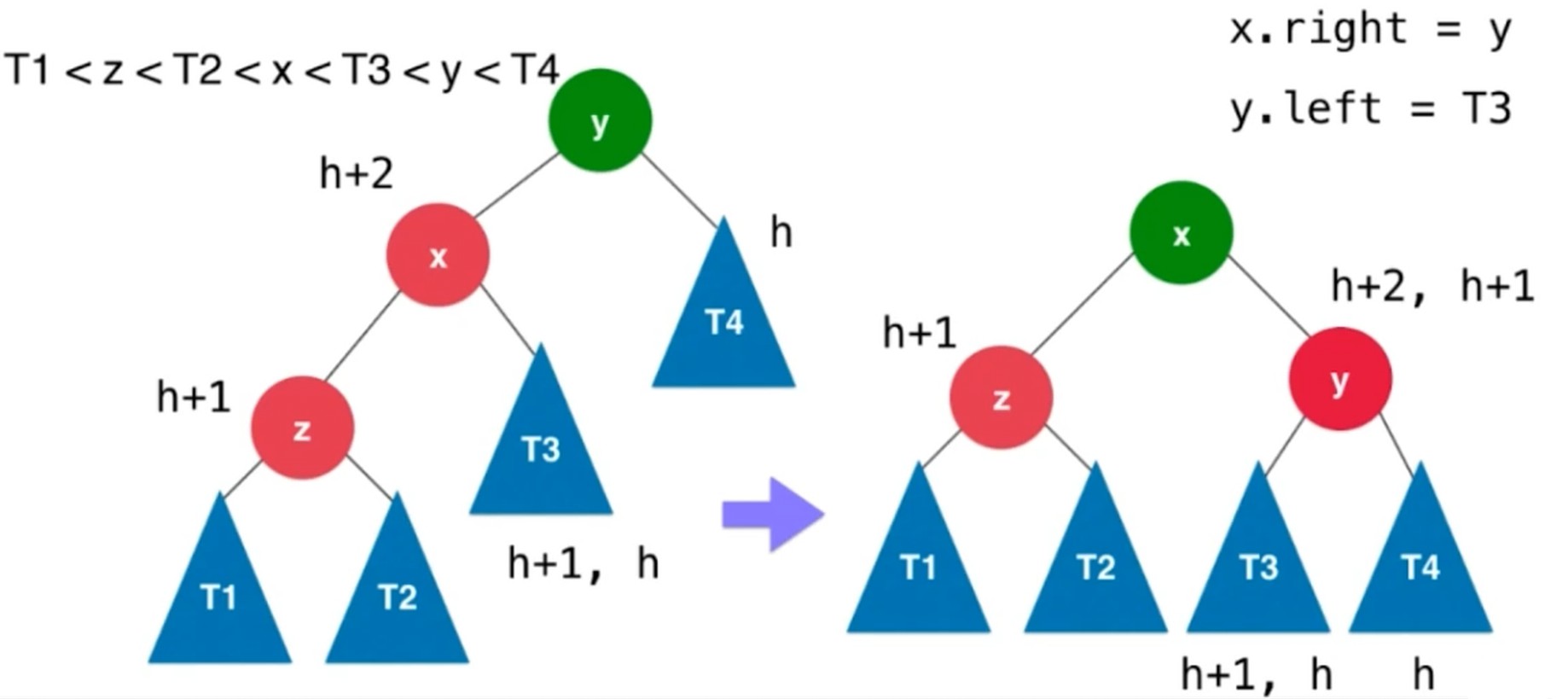
对于y来说, 顺时针转到了x的右侧. 左子树比右子树大2.
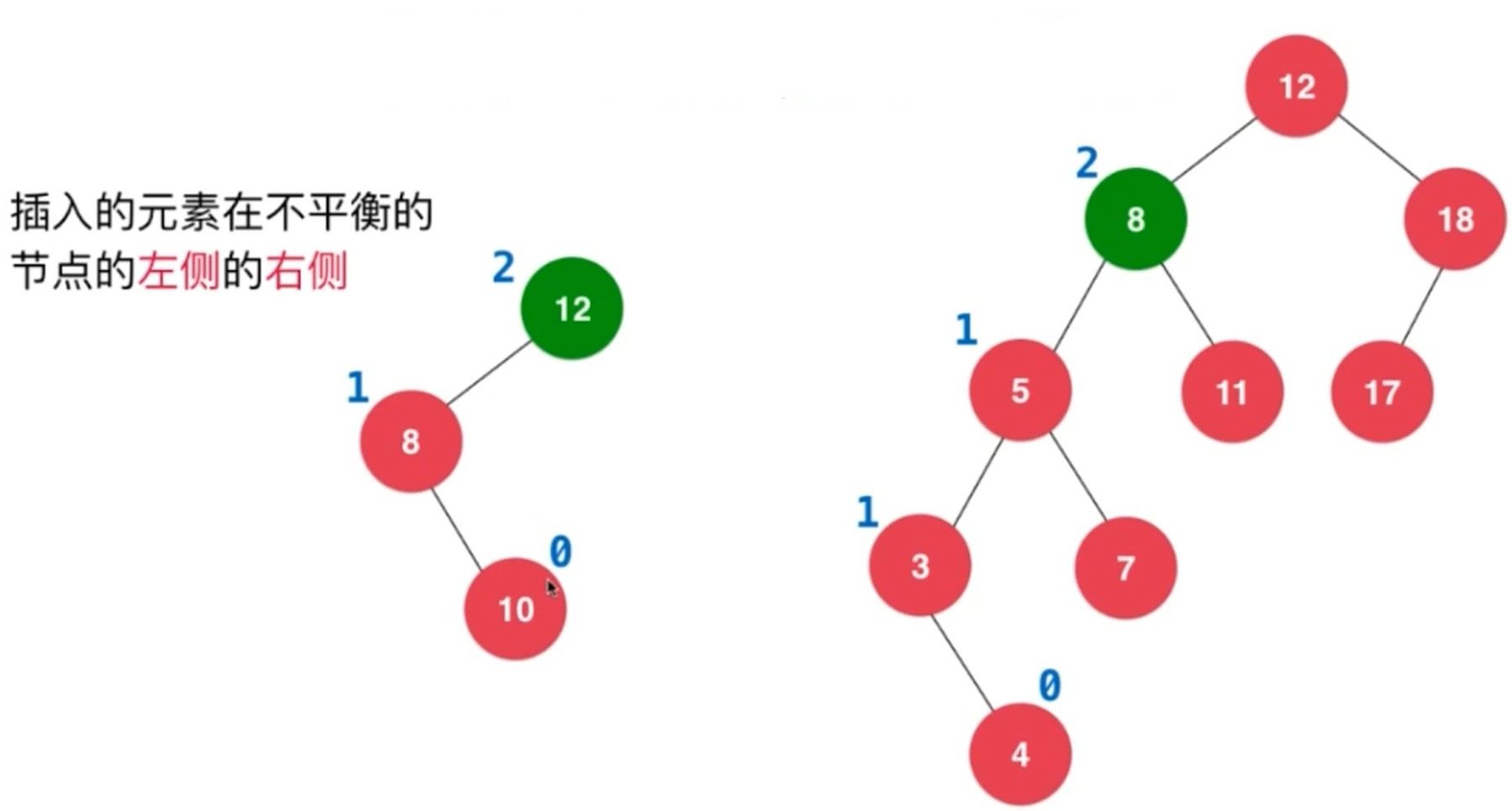
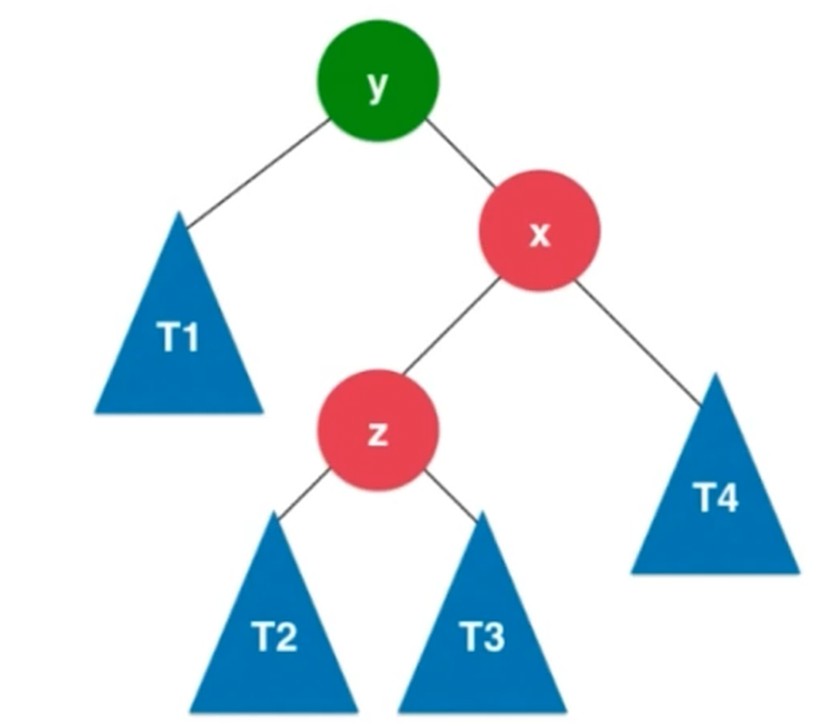
左旋转, 插入元素在不平衡的节点的右侧的右侧.
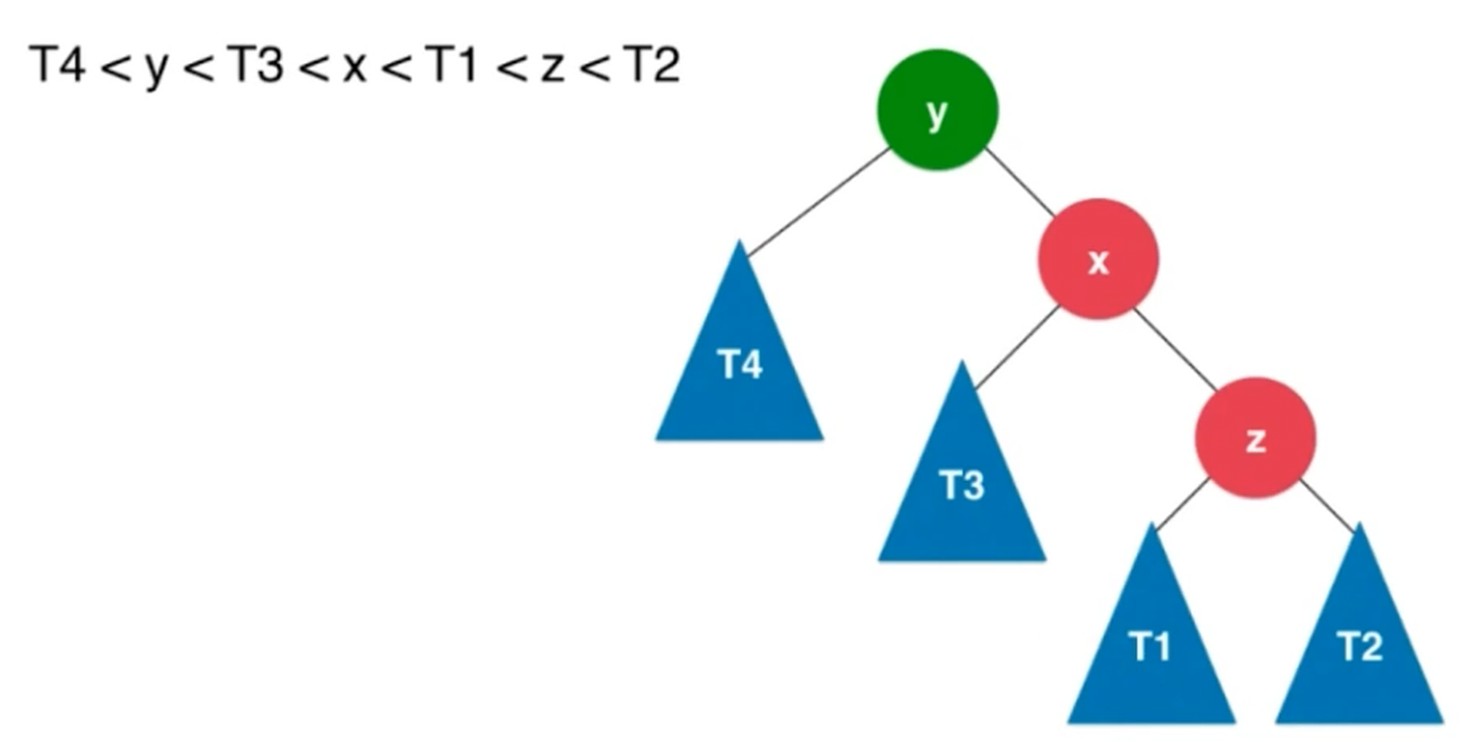
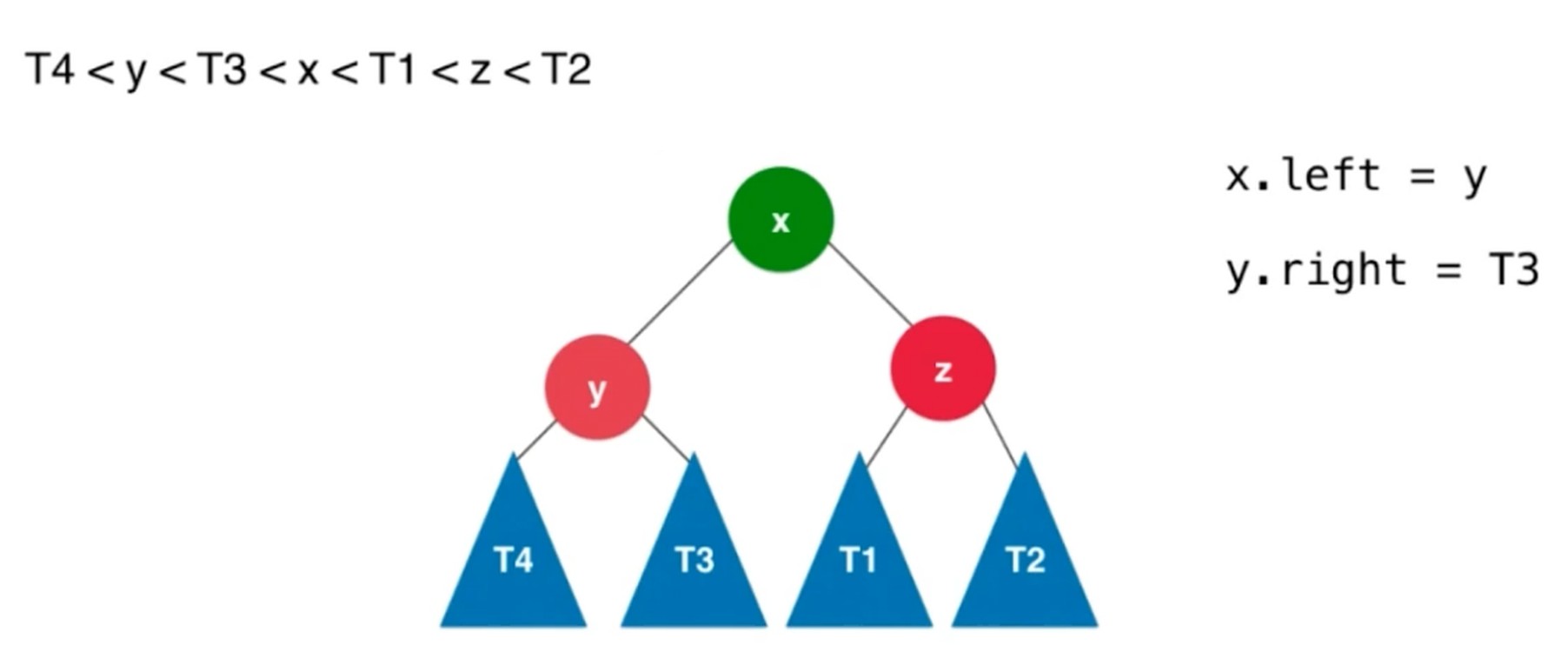
不平衡节点的左侧和右侧
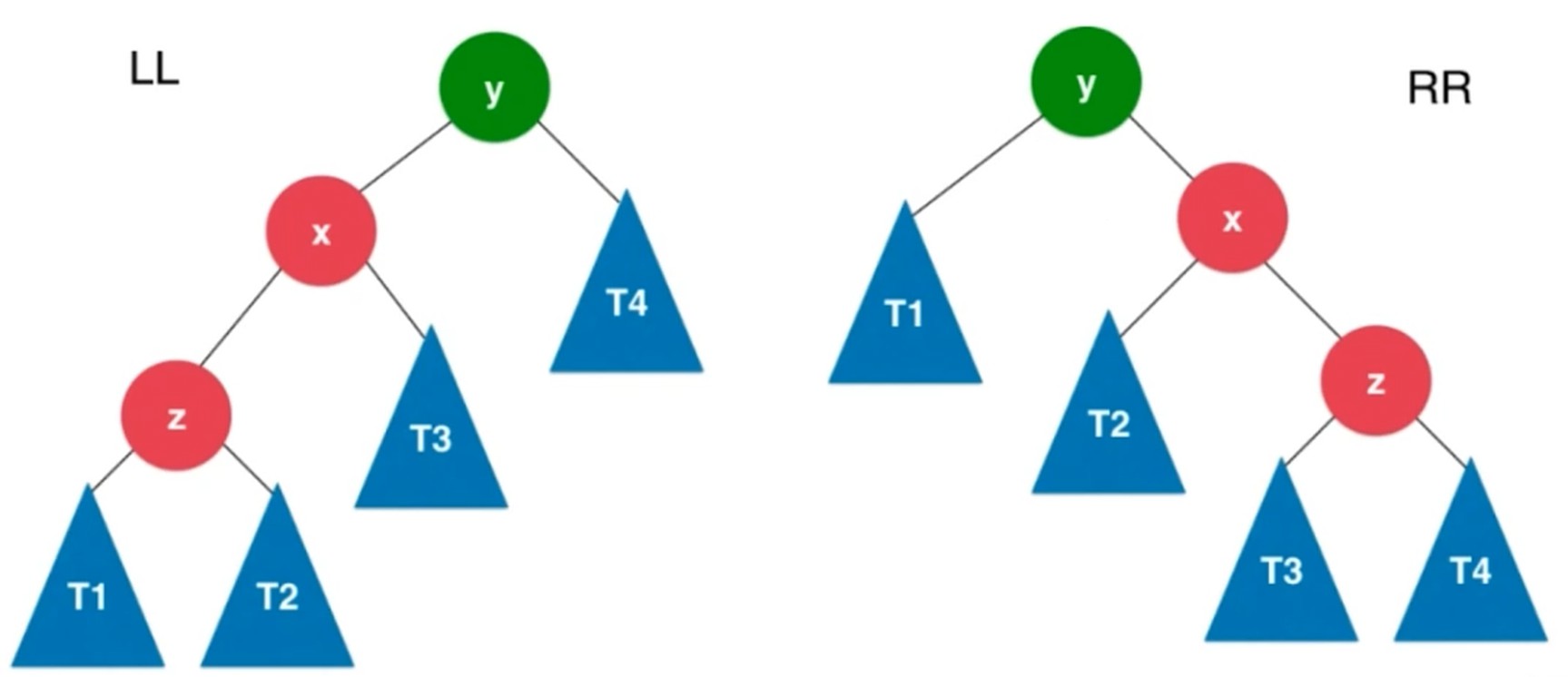
LL, RR, LR 和 RL
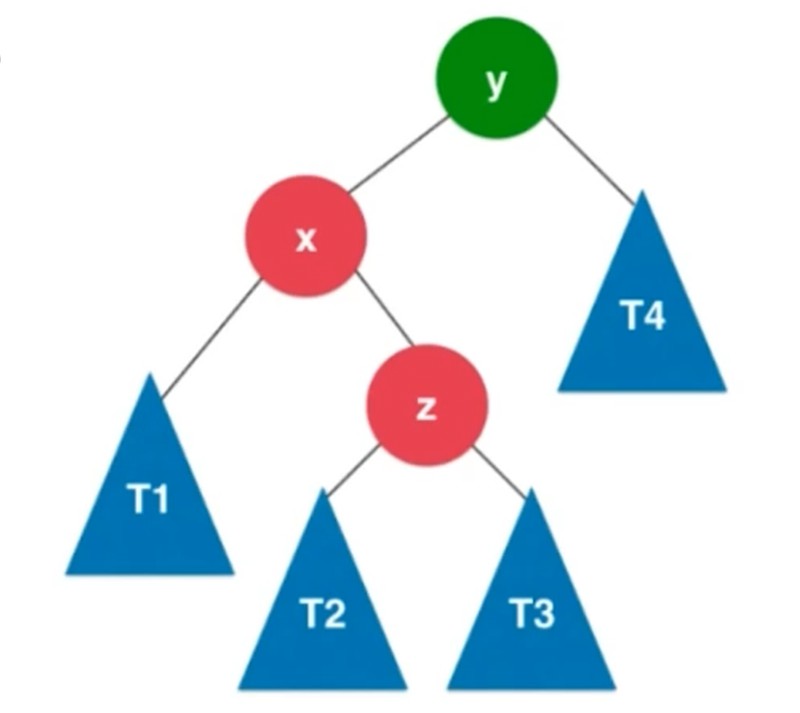
转成LL之后再右旋转
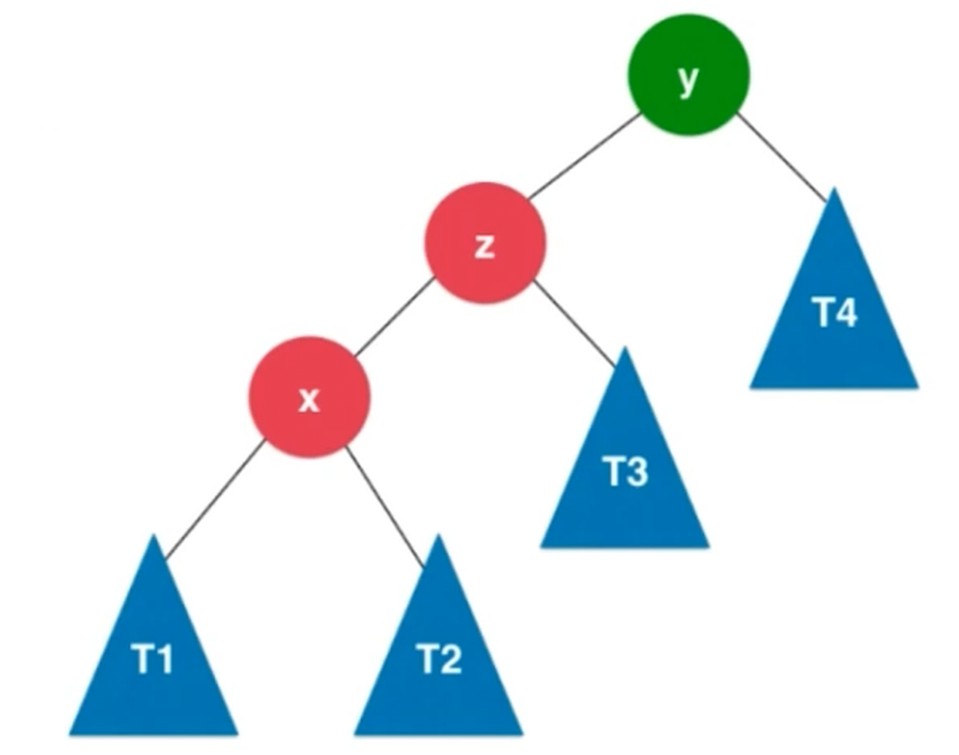
RL的情况, x节点右旋转之后, 转成RR的情况, 之后y节点左旋转
红黑树 Red Black Tree
- 红黑树与2-3树的等价性
- 2-3树和红黑树之间的关系
2-3树
- 满足二分搜索树的基本性质
- 节点可以存放一个元素或者两个元素
- 每个节点都有2个或者3个孩子

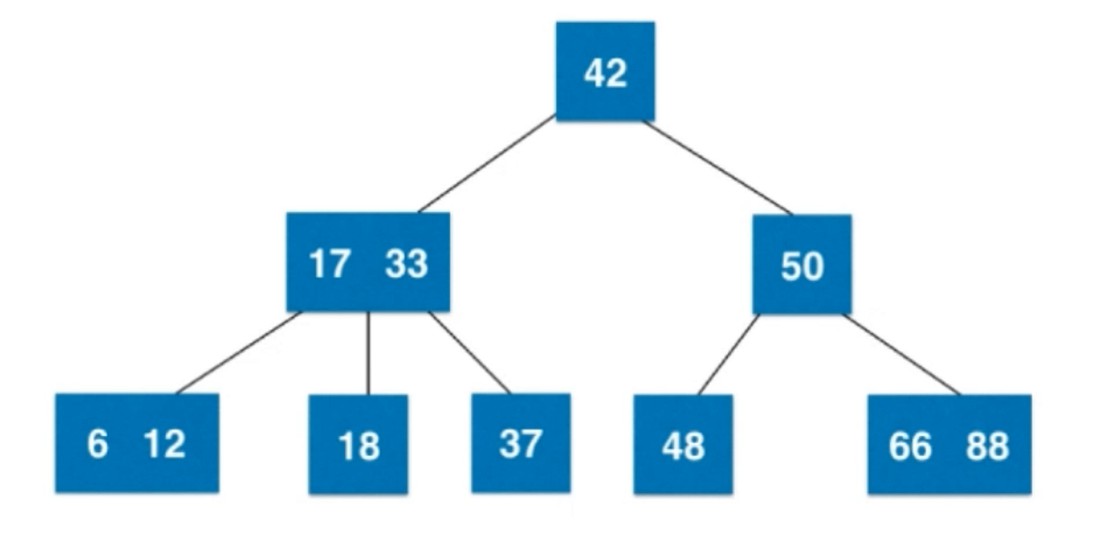
2-3树是一棵绝对平衡的树. 二分搜索树, 可能退化成链表; 对于堆, 虽然是完全二叉树, 但是最后一层没有填满, 所以不是绝对平衡; 线段树, 叶子节点分布在最后一层或者倒数第二层; 并查集, 左右子节点树相差不超过1, 相对是宽松的, 达不到绝对平衡.
添加节点不会添加到空的位置, 会和已经存在的节点合并, 根据大小判断放在左边还是右边.
只有一个节点的时候, 这个节点是2-节点, 加多个节点后就变成3-节点了. 如果再多一个就4-节点了, 不满足2-3树的要求.
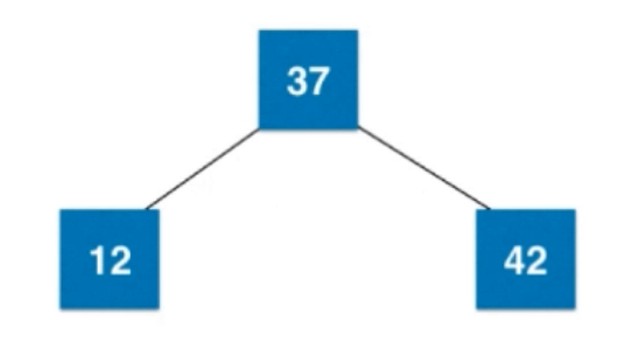
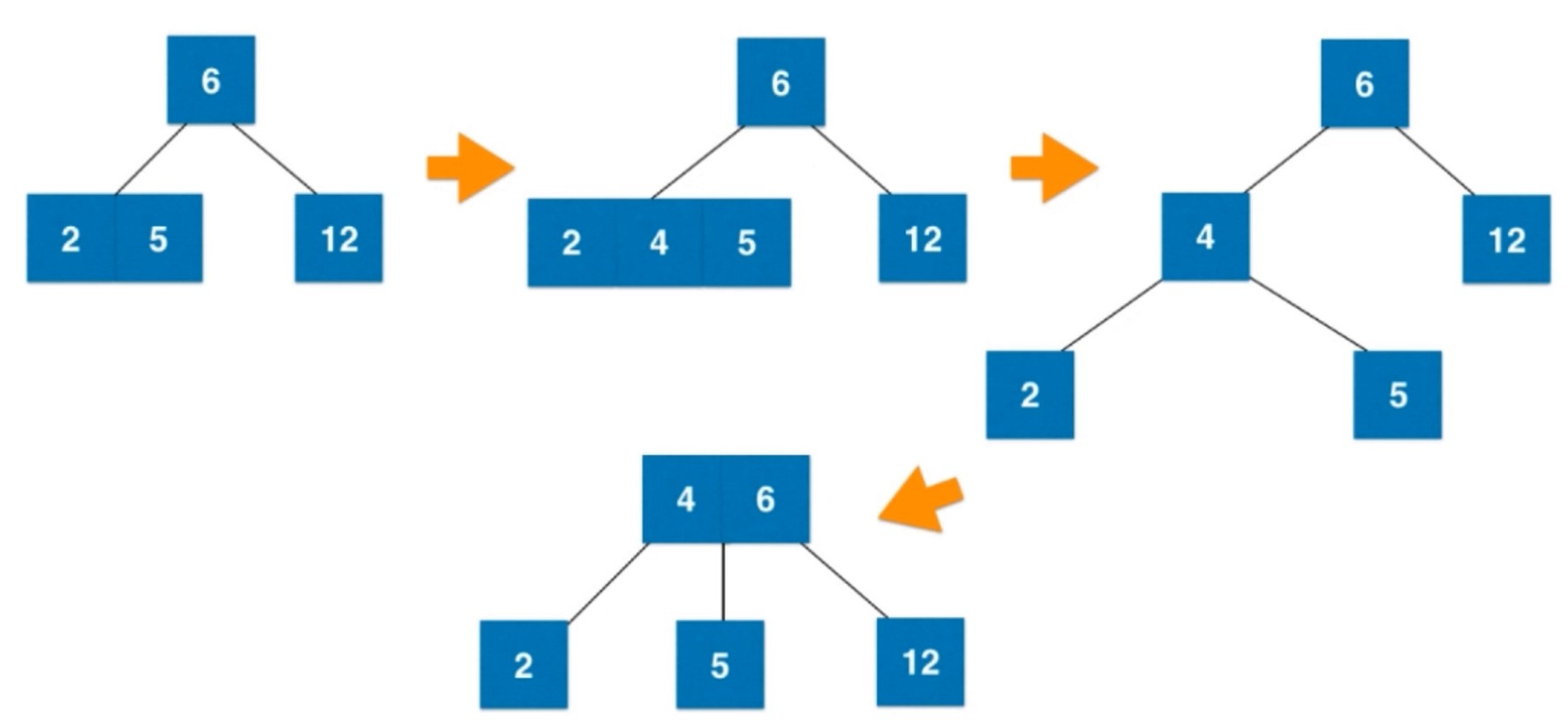
再来一个元素18, 比37小, 添加到左子树, 而比12大, 应该添加在右子树, 但是该节点右子树还是空, 所以和12进行合并, 放在右边, 形成一个3-节点.
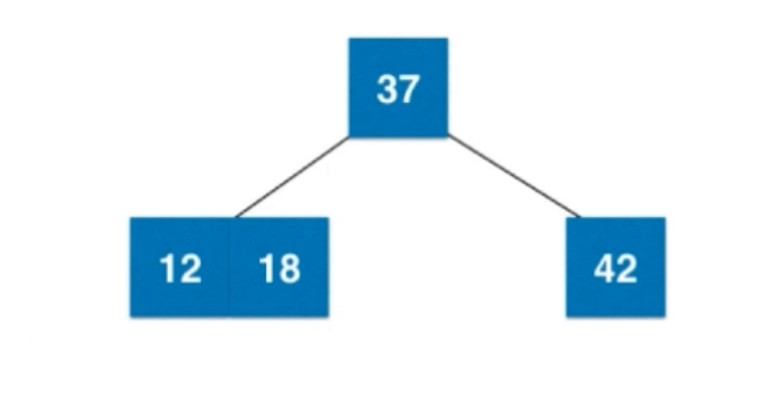
来个6, 比12小, 应该12的左边, 但是又为空, 所以进行合并, 合并之后, 因为是四节点了, 所以进行拆解.
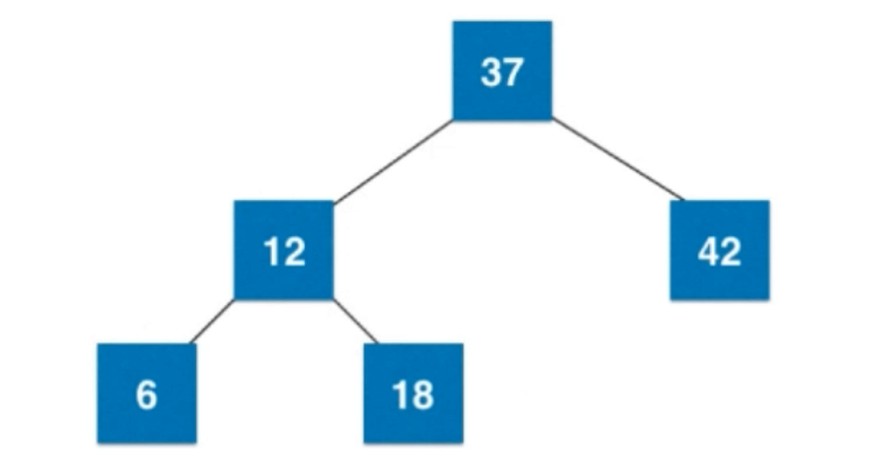
12向上和父亲节点37融合.
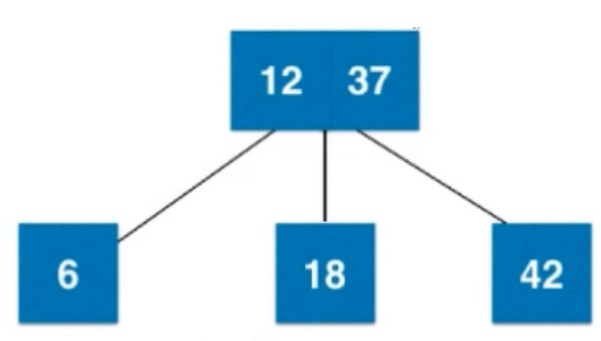
再添加一个11, 会和6融合, 放在右边.
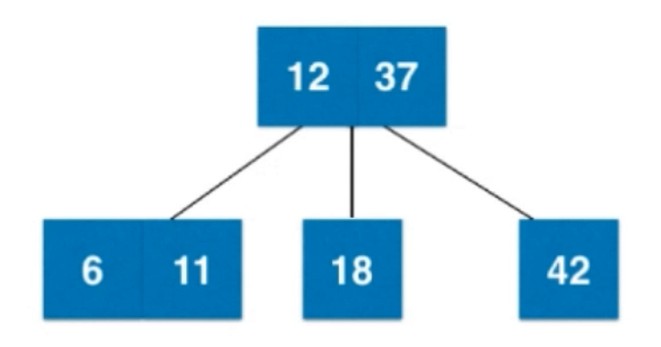
添加个5, 和6所在节点融合之后, 变成4-节点了, 进行拆解.
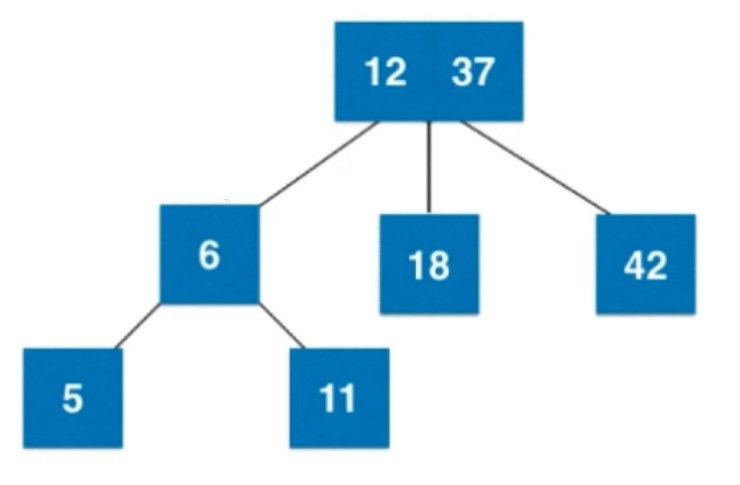
拆解之后, 6向上和父亲节点融合.
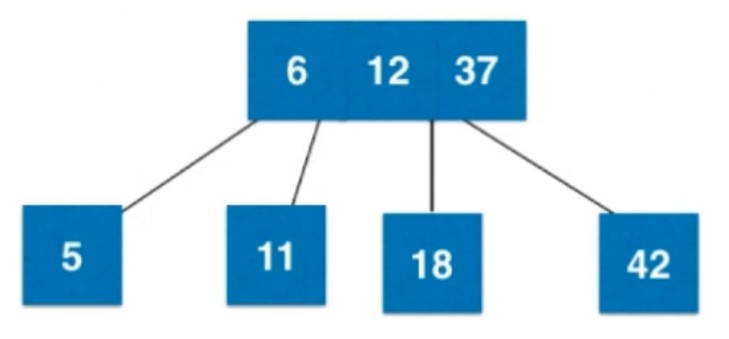
超过了2-3树的4-节点限制, 进行拆分, 拆之后, 所有节点都是2-节点了.
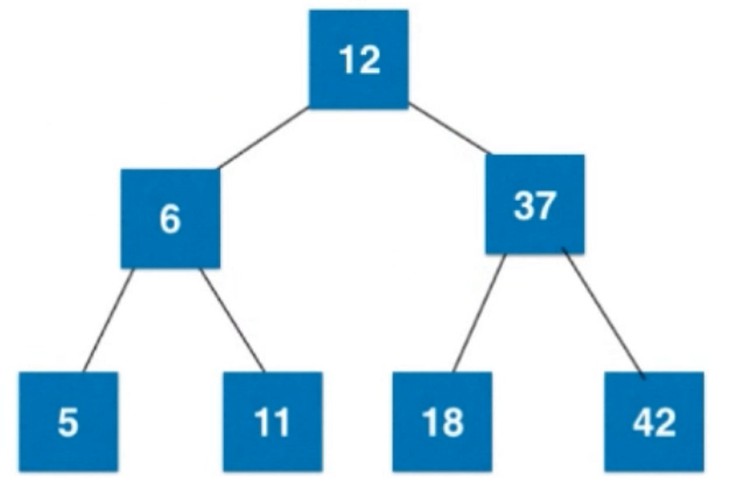
以上演示是从大到小顺序添加元素的, 如果是二分搜索树的话, 已经非常偏斜了.
总结:
插入一个2-节点, 直接融合成一个3-节点, 如果是插入一个3-节点, 先融合, 再拆分变形.
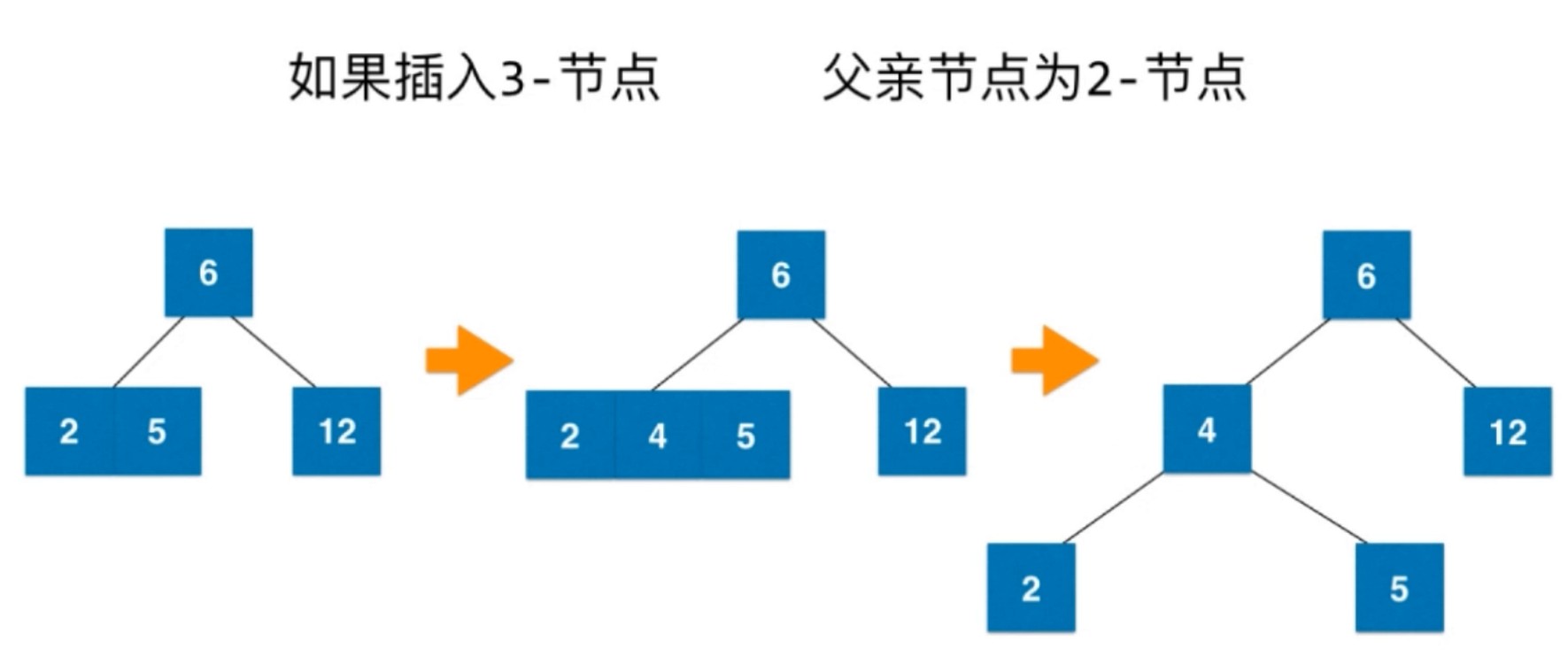
之后4和父亲节点融合, 形成一个3-节点.
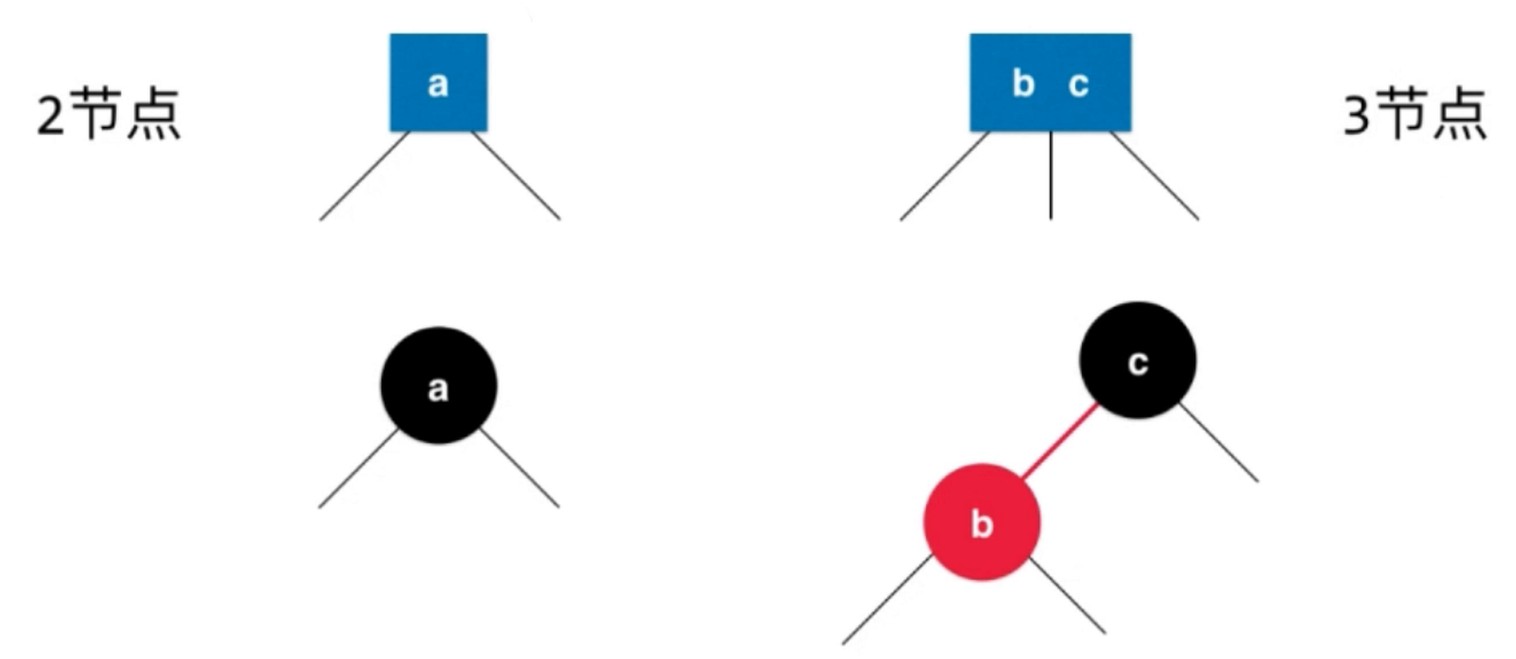
如何表示, 让b变成红色, 其实表达的是 b和a 连接的边是红色的, 在2-3树中是一个并列的关系. 巧妙地把边的信息放在了节点上.
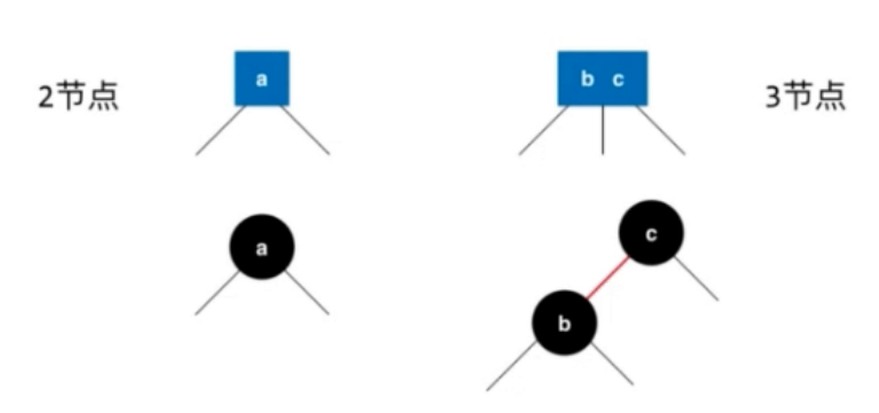
所有红色节点都是左倾斜的.
红黑树和2-3树的等价性
红黑树和2-3树
例子
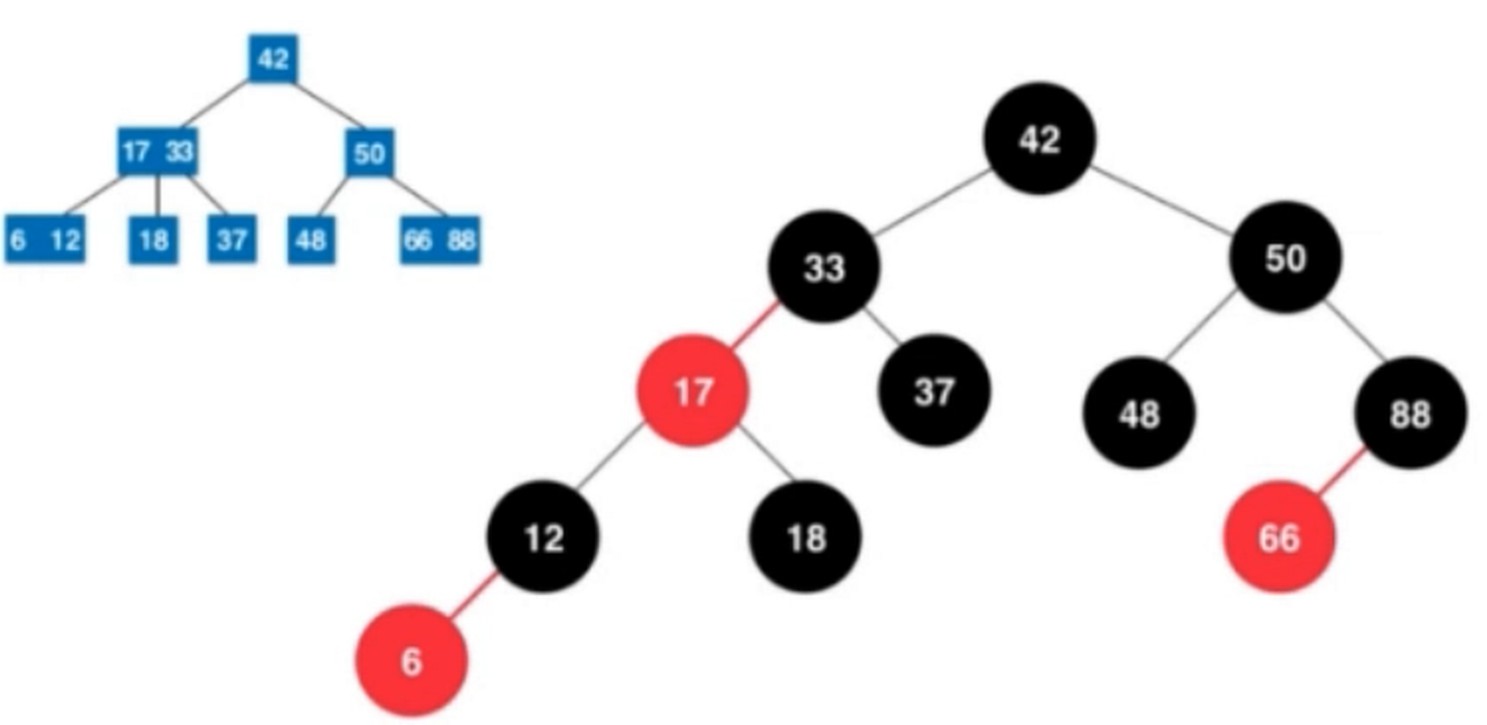
算法导论中的红黑树
- 每个节点或者是红色的, 或者是黑色的
- 根节点是黑色的
- 每一个叶子节点(最后的空节点)是黑色的
- 如果一个节点是红色的, 那么他的孩子节点都是黑色的.(有红节点, 所以对应是2-3树的3-节点, 而红色连接的是2节点或者3节点, 2-节点是黑色的, 连接是3-节点的话, 也是先连接上黑色的节点)
- 从任意一个节点到叶子节点, 经过的黑色节点数量是一样的
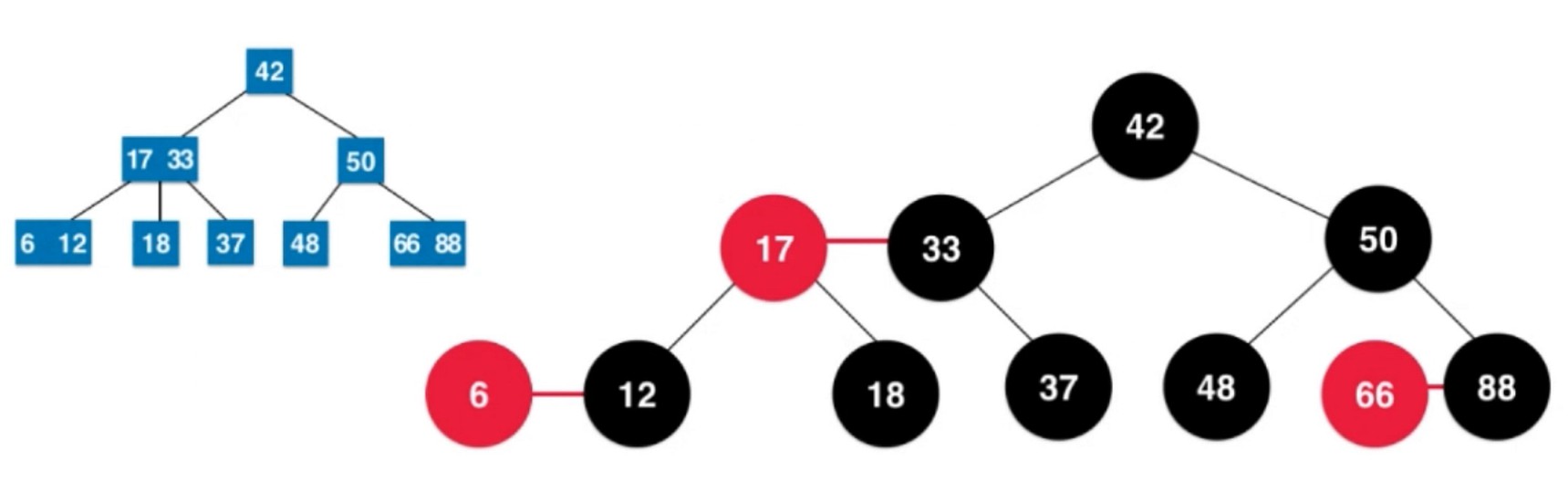
一个黑色的右节点一定是黑色的.
红黑树是保持”黑平衡”的二叉树.
严格来说, 红黑树不是平衡二叉树. 但是左右节点的黑色节点之间的高度保持这绝对平衡.
最大高度: 2logn, 而2是常数, 在复杂度分析是忽略的, 所以时间复杂度是 O(logn).
红黑树的最大高度要比AVL树的高, 所以在元素查找时会比AVL树慢一点, 但是红黑树的增加和删除元素相比AVL要更快, 所以如果是一些经常要修改的数据, 更适合使用红黑树. 如果数据是查询更多的话, AVL树是更适合的.
红黑树添加元素
2-3树中添加一个新元素
- 添加进2-节点, 形成以一个3-节点
- 添加进3-节点, 暂时形成一个4-节点, 然后进行变形处理
永远添加红色节点
红黑树根节点必须是黑色的.
向上融合的元素是红色节点.

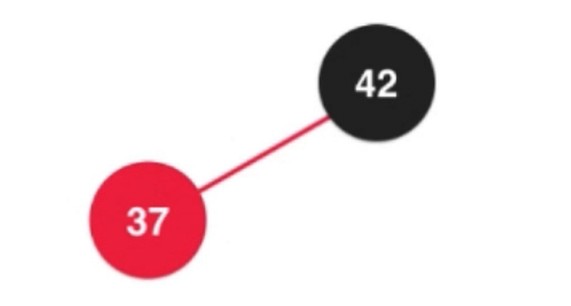
如果是大于的, 不能直接放右边, 红黑树规定所有红色都是向左倾斜的. 此时需要进行左旋转.
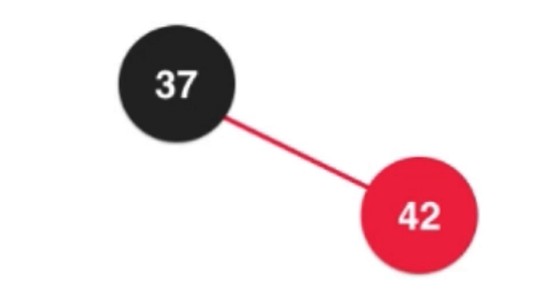
左旋转后
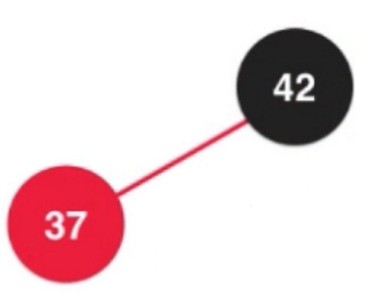
左旋转具体流程. x的是node的右子树, 所以这棵树的所有元素都比node大.
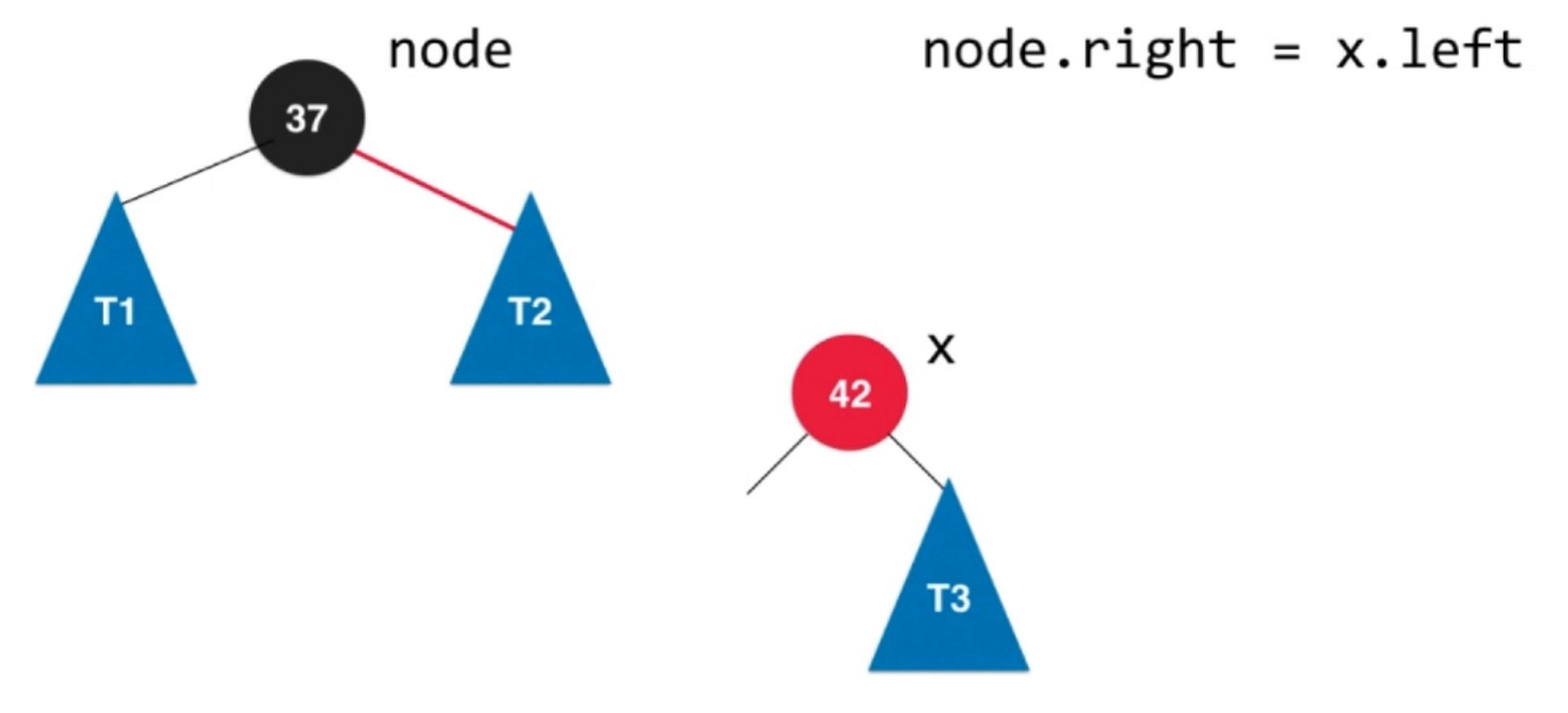
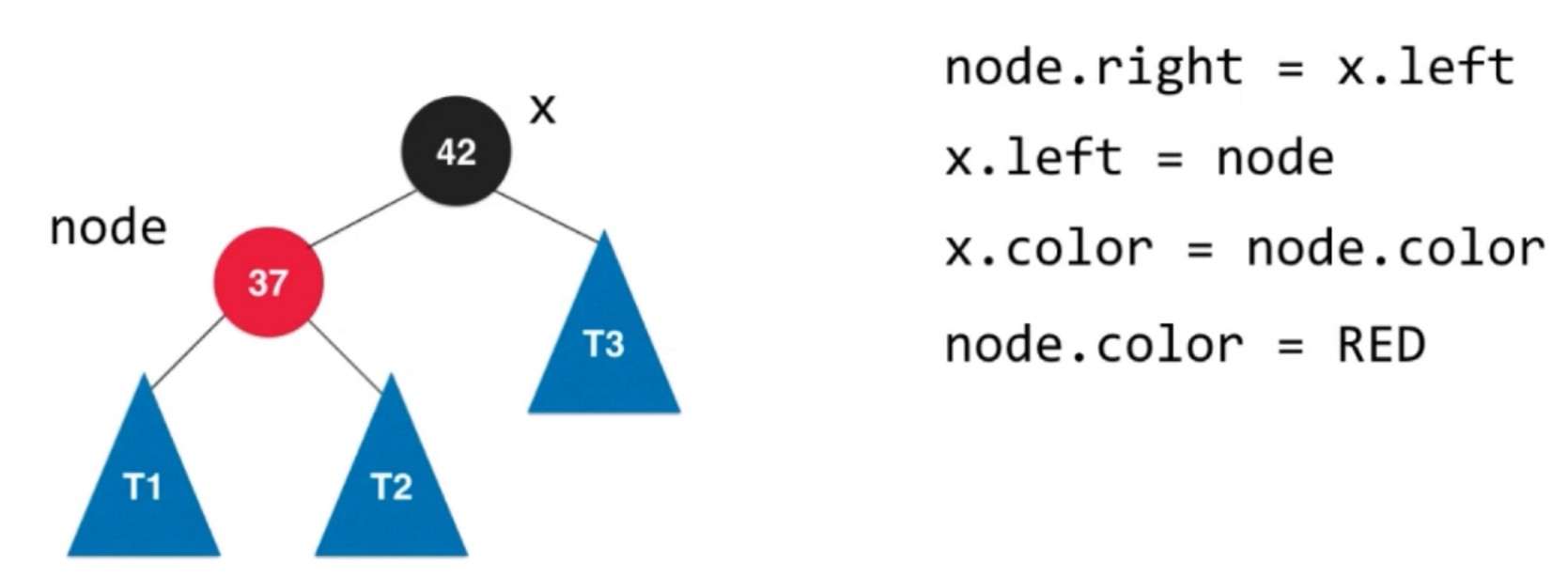
颜色翻转(flipColors)和右旋转
在上面的基础上, 添加一个大于42的节点, 产生临时4-节点
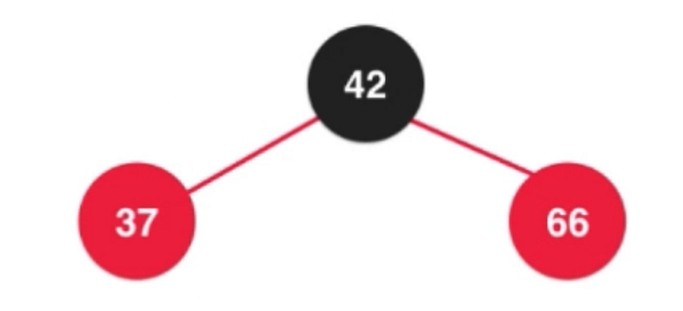
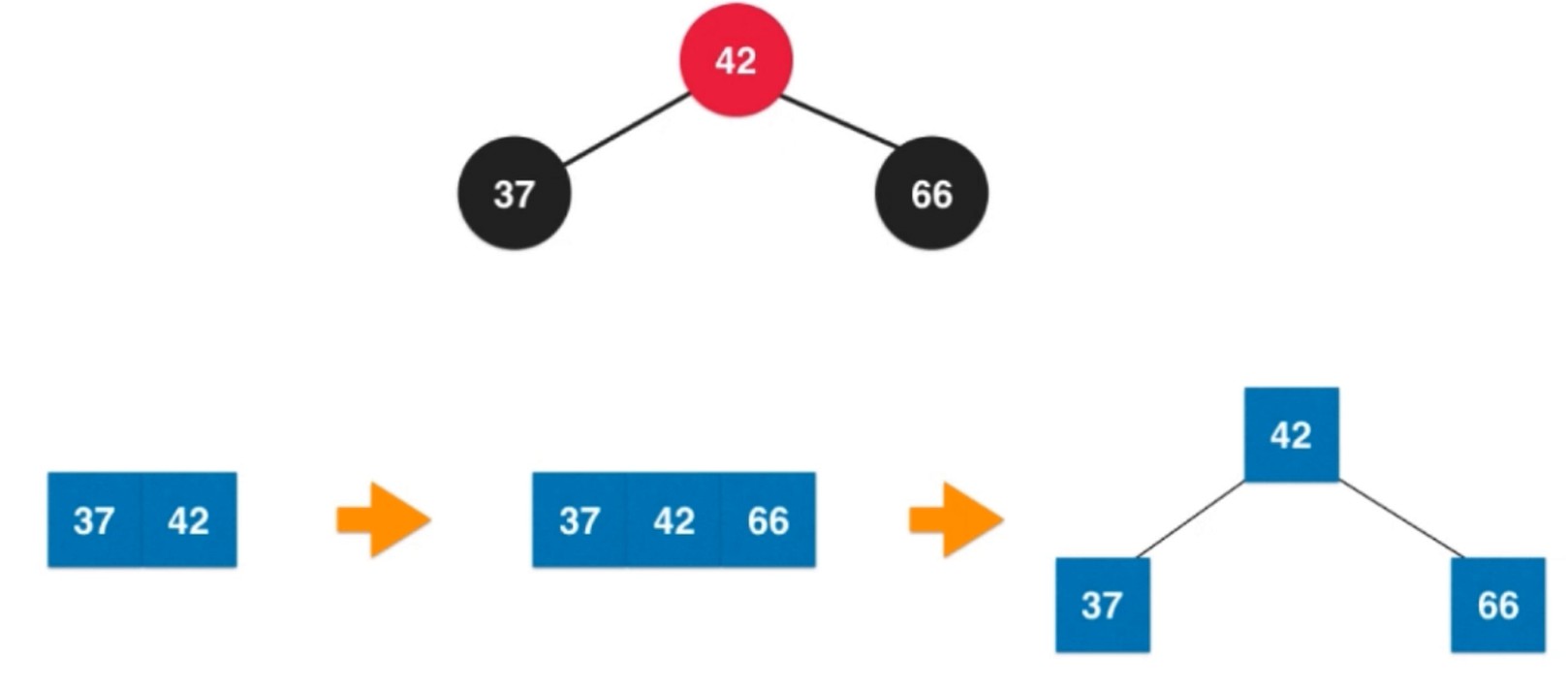
红色节点 代表和父亲节点进行融合.
添加一个小于37的节点. 使用 右旋转 解决.
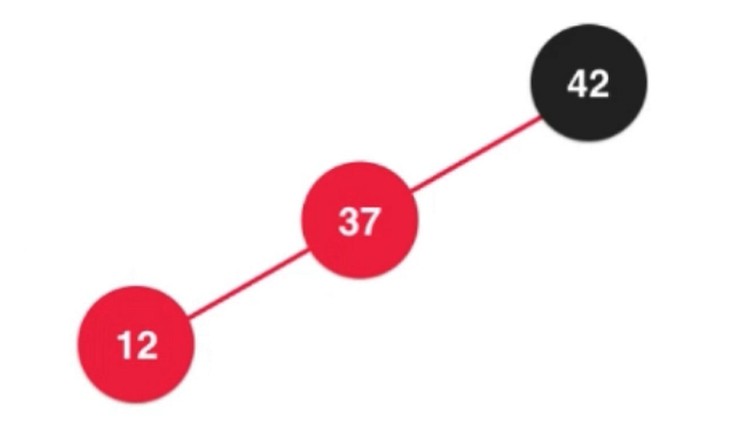
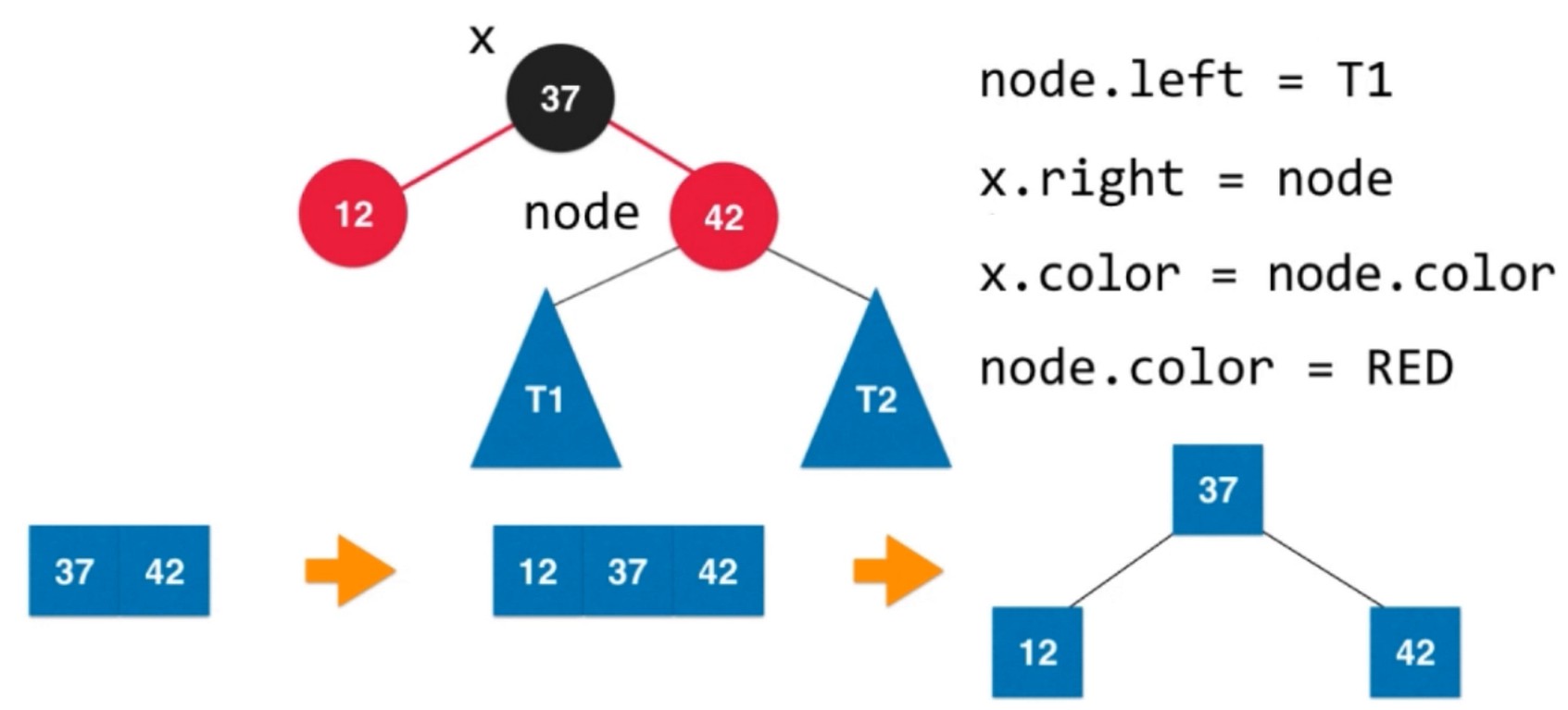
之后进行颜色翻转.
如果插入是一个介于两者之间的数, 先左旋转, 再右旋转, 最后颜色翻转.
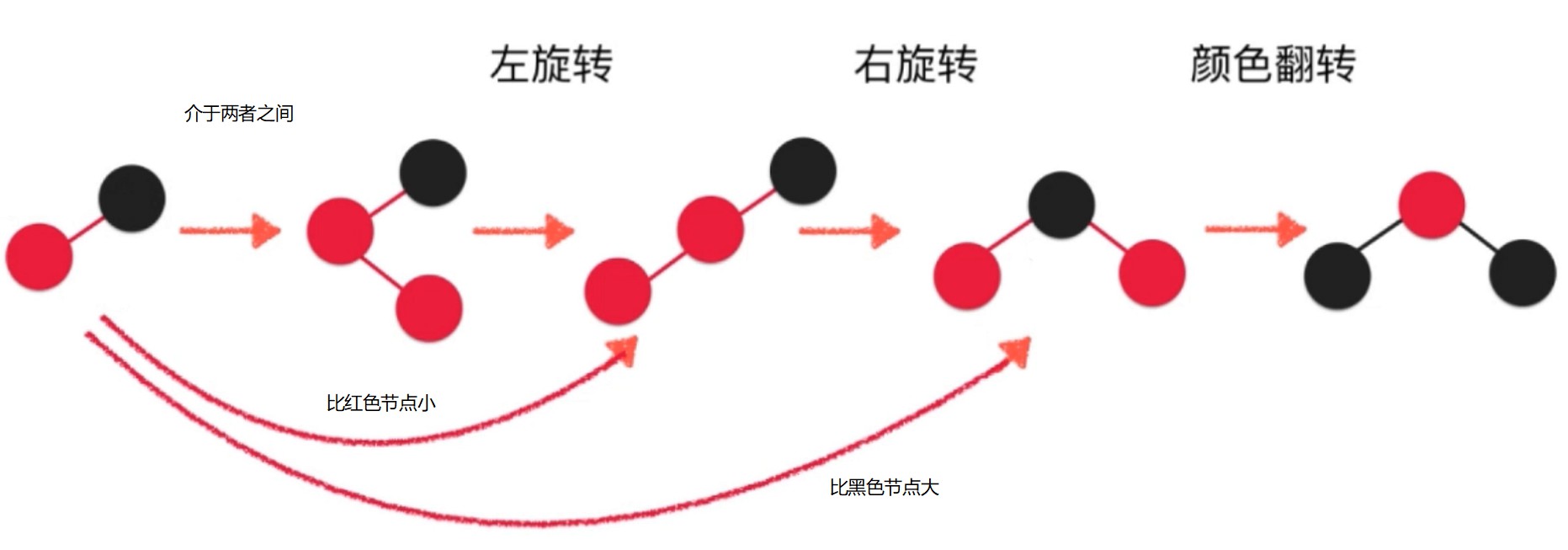
维护时机, 和 AVL 树一样, 添加节点后回溯向上维护.
红黑树性能
- 二分搜索树
- 对于完全随机的数据, 没什么问题
- 极端情况退化成链表(或者高度不平衡)
- AVL
- 适合查询较多的使用情况
- 红黑树
- 牺牲了平衡性(2logn的高度)
- 统计性能更优(综合增删改查所有的操作)
另外一种统计性能优秀的树结构: Splay Tree 伸展树.
java.util中的TreeMap和TreeSet就是基于红黑树的.
哈希表 Hash Table
题目: 字符串中第一个唯一字符
s = “leetcode”, 返回0
s = “loveleetcode” 返回2
public int firstUniqChar(String s) {
// 哈希表
// 每一个字符都和一个索引相对应
int[] freq = new int[26];
// 把26个小写字母映射到0-25
// 计算出每个字符出现的频率
s.chars().forEach(c -> freq[c - 'a']++);
int[] res = s.chars().filter(c -> freq[c - 'a'] == 1).toArray();
return res != null ? res[0] : -1;
}

而转换成索引的函数就是叫做哈希函数.
问题: 很难保证每一个”键”通过哈希函数的转换对应不同的”索引”.
这种问题叫做 哈希冲突.
哈希表充分体现了算法设计领域的经典思想: 空间换时间.
哈希表是时间和空间之间的平衡.
哈希函数设计
“键”通过哈希函数得到的”索引”分布越均匀越好.
整型
- 取模, mod的数值不够好会导致分布不均匀; 没有利用所有信息; 具体问题具体分析.
一个简单的解决方法: 模一个素数

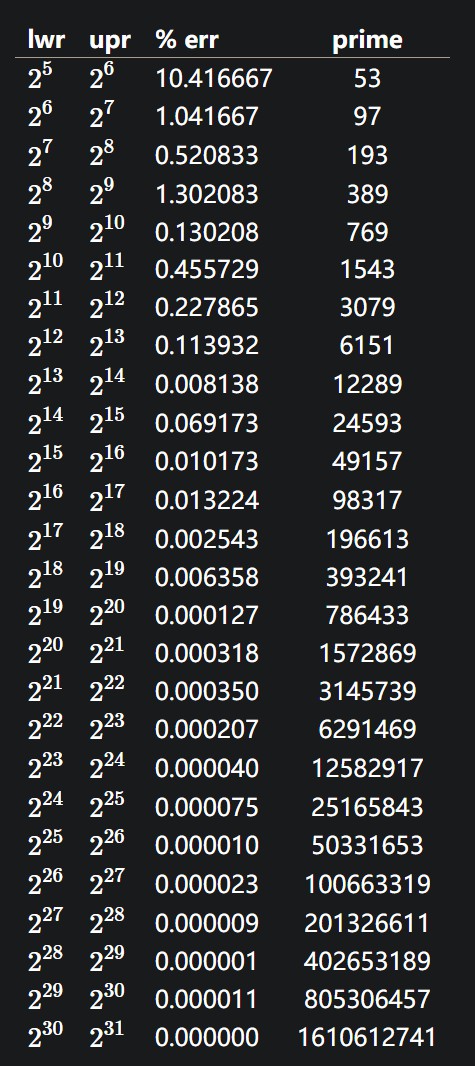
浮点型
计算机中都是32位或者64位二进制表示数值的,只不过计算机解析成了浮点数.
对浮点型占用的01进行处理.
字符串 转成整型处理

转成代码
int hash = 0;
for(int i=0; i<s.length(); i++)
hash = (hash * B + s.chatAt(i)) % M
复合类型
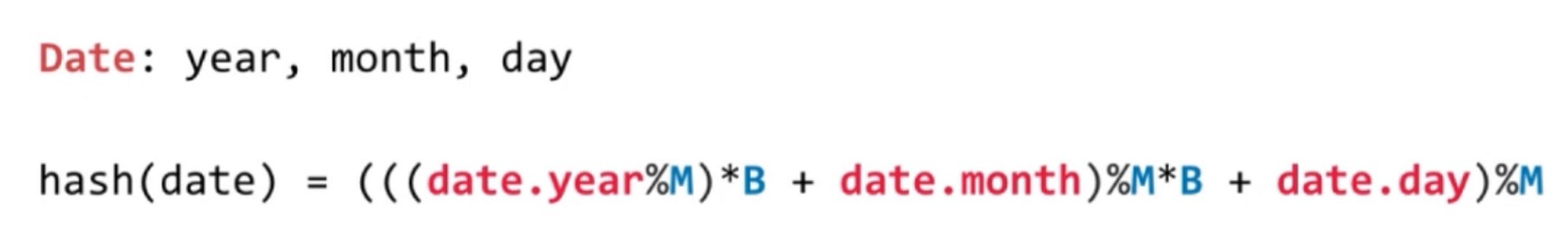
三个原则
- 一致性: 如果 a==b, 则hash(a)==hash(b)
- 高效性: 计算高效简便
- 均匀性: 哈希值均匀分布
java中的hashCode只是产生哈希值的, 如果产生哈希冲突了, 需要比较两个对象是否一样, 需要重写 equals().
哈希冲突处理
链地址法–Seperate Chaining

(hashCode(k1) & 0x7fffffff) % M : 实际就是把K1哈希之后取整, 然后取模
哈希值一样的元素用链连接起来. 而这个叫做查找表, 查找表可以用平衡树, 也可以用链表.
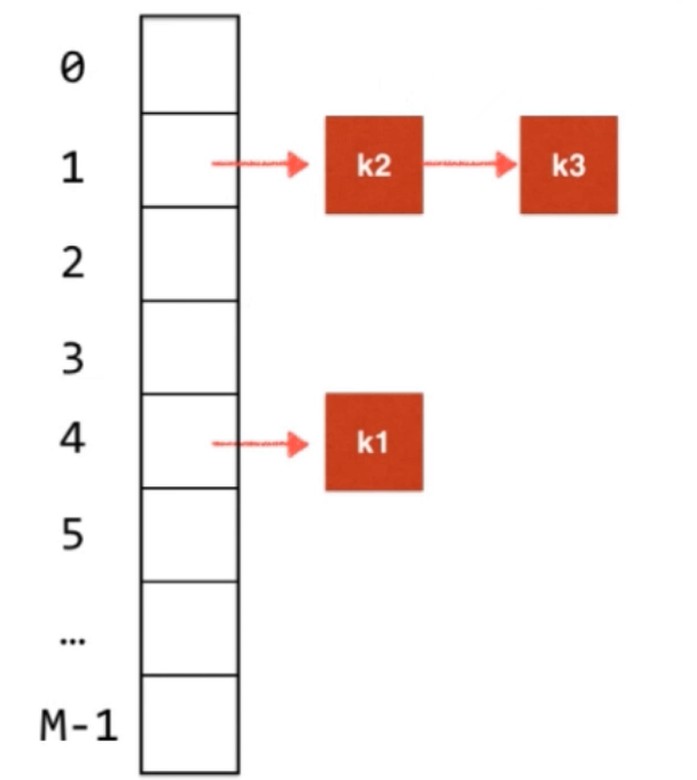
例如: HashMap就是一个TreeMap数组
Java8之前, 每个位置对应一个链表
Java8之后, 当哈希冲突到一个程度, 每个位置从链表转成红黑树. 原因是当数据量小的时候, 链表更有优势. 注意的是, 转成红黑树要求这个对象是有序的.
开放地址法–Open Addressing
链地址法, 地址是封闭的, 地址只属于等于此哈希值的元素.
哈希冲突的话直接下放下一个位置.
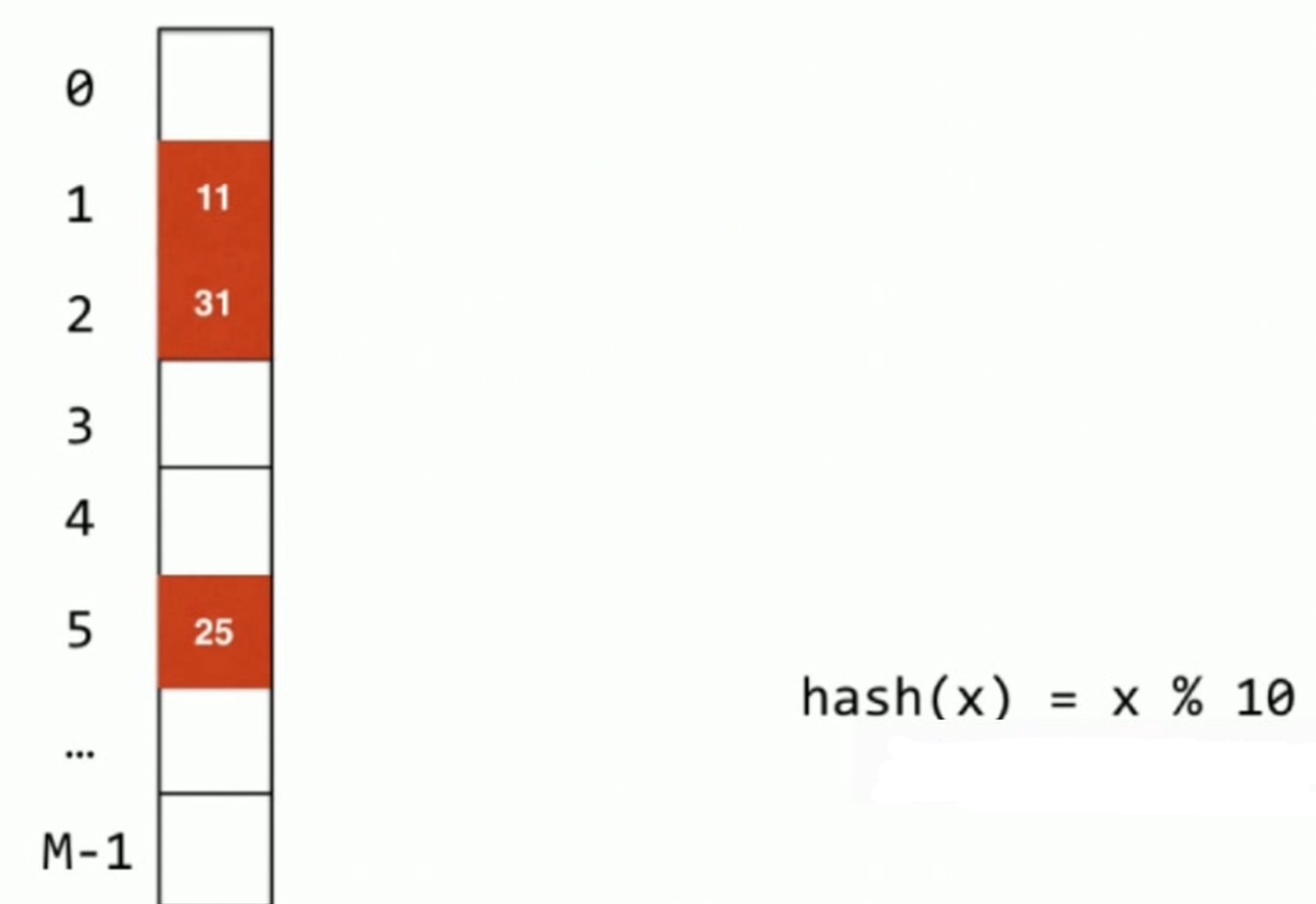
每一个地址对元素都是开放的. 上面的方法叫做 线性探测, 遇到哈希冲突+1
但是元素多后性能会明显下降, 改进方案 平方探测. 遇到哈希冲突 +1 +4 +9 +16…因为步长是某数值的平方, 所以叫平方探测.
二次哈希法
遇到哈希冲突的时候 hash2(key), 使用另外的hash函数计算出位置.
负载率: 哈希表中, 元素总数占地址数的百分比, 当负载率到一定程度时, 进行扩容或者缩容
再哈希法–Rehashing
时间复杂度分析

哈希碰撞攻击.
如何做到O(1), 使用动态数组的方式. 动态数组的均摊复杂度, 平均复杂度O(1)
平均每个地址承载的元素多于一定程度, 扩容. N/M >= upperTol
平均每个地址承载的元素少过一定程度, 即缩容. N/M < lowerTol

扩容 M -> 2M, 明显不是素数了, 解决方案, 使用上面的*素数选择.
哈希表虽然均摊复杂度为O(1), 就是因为放弃维护顺序性, 相对于树的结构牺牲了顺序性. 有得必有失.
集合, 映射
- 有序集合, 有序映射 平衡树
- 无序集合, 无序映射 哈希表
总结
线性结构: 动态数组, 链表, 普通队列, 栈, 哈希表
树形结构: 二分搜索树, AVL, 红黑树, 堆, 线段树, Trie(字典树), 并查集
图结构: 邻接表, 邻接矩阵
更多数据结构: 双端队列; 随机队列; 最大最小队列; 双向链表; 循环链表; 跳跃表; 后缀数组; K-D树; Splay树; B树